SIGNIFICADO Y USO DE LOS NÚMEROS NÚMEROS ENTEROS
Significado y uso de las operaciones básicas con números enteros
Los números son signos o conjuntos de signos que permiten expresar una cantidad con relación a su unidad.
El concepto proviene del latín numĕrus y posibilita diversas clasificaciones que dan a lugar a conjuntos como los números naturales (1, 2, 3, 4…), los números racionales y otros.
Los números enteros abarcan a los números naturales (los que se utilizan para contar los elementos de un conjunto), incluyendo al cero y a los números negativos (que son el resultado de restar a un número natural otro mayor). Por lo tanto, los números enteros son aquellos que no tienen parte decimal (es decir que 3,28, por ejemplo, no es un número entero).
Además de todo lo expuesto tampoco podemos obviar el hecho de que los números enteros nos sirven igualmente para establecer la altura de un monumento o de un elemento natural. Así, por ejemplo, podemos hablar de que el Mulhacén es el pico más alto que existe en la Península Ibérica pues está situado a 3.478 metros sobre el nivel del mar mientras que el Teide es el más alto de España al conseguir alcanzar los 3.718 metros.
Los números enteros negativos tienen diversas aplicaciones prácticas. Con ellos se puede señalar una temperatura bajo cero (“En estos momentos, la temperatura en Bariloche es de -10º”) o una profundidad bajo el nivel del mar (“El barco hundido fue hallado a -135 metros”).
Es importante tener en cuenta que los números enteros son el resultado de las operaciones más básicas (suma y resta), por lo que su utilización se remonta a la antigüedad. Los matemáticos hindúes del siglo VI ya postulaban la existencia de números negativos.
De la misma forma, tampoco podemos pasar por alto el hecho de que también podemos llevar a cabo tareas de multiplicación con los llamados números enteros. En este caso es importante subrayar que ahí hay que realizar la determinación, por un lado, de lo que son los signos de los números que participan en la operación y, por otro lado, del producto de los valores absolutos.
Así, en el primer caso, en el de los signos, hay que subrayar una serie de reglas que hay que tener muy en cuenta. De tal manera que + por + es igual a +; – por – es igual a +; + por – es igual a -; y – por + es igual a -. Ejemplos para entender estas reglas expuestas pueden ser los siguientes: +5 x +6= +30; -8 x -2= +16; +4 x -
2= -8; -6 x +3= – 18.
En materia de multiplicación hay que subrayar además que existen diversas propiedades como son la asociativa, la distributiva o la conmutativa.
La noción de números enteros fue establecida ya que se trata de números que permiten representar unidades no divisibles, como una persona o un país (no puede decirse “En mi casa viven 4,2 personas” o “El próximo campeonato mundial tendrá la participación de 24,69 países”). Los números con decimales, en cambio, pueden indicar unidades divisibles.
Una operación es un conjunto de reglas que permiten obtener otras cantidades o expresiones.
Las siete operaciones básicas de la Aritmética son:
Suma
La operación suma consiste en obtener el número total de elementos a partir dos o más cantidades.
a + b = c
Los términos de la suma, a y b, se llaman sumandos y el resultado, c, suma. Propiedades de la suma
. Asociativa:
El modo de agrupar los sumandos no varía el resultado. (a + b) + c = a + (b + c)
Conmutativa:
El orden de los sumandos no varía la suma.
a + b = b + a
Elemento neutro:
El 0 es el elemento neutro de la suma porque todo número sumado con él da el mismo número.
a + 0 = a
Elemento opuesto:
Dos números son opuestos si al sumarlos obtenemos como resultado el cero.
a − a = 0
El opuesto del opuesto de un número es igual al mismo número. La suma de números naturales no cumple esta propiedad.
Resta
La resta o sustracción es la operación inversa a la suma. a - b = c
Los términos que intervienen en una resta se llaman: a, minuendo y b, sustraendo. Al resultado, c, lo llamamos diferencia.
Propiedades de la resta No es Conmutativa :
a − b ≠ b – a
Multiplicación
Multiplicar dos números consiste en sumar uno de los factores consigo mismo tantas veces como indica el otro factor.
a · b = c
Los términos a y b se llaman factores y el resultado, c, producto. Propiedades de la multiplicación:
Asociativa :
El modo de agrupar los factores no varía el resultado
(a · b) · c = a · ( b · c)
Conmutativa:
El orden de los factores no varía el producto.
a · b = b · a
Elemento neutro:
El 1 es el elemento neutro de la multiplicación porque todo número multiplicado por él da el mismo número.
a · 1 = a
Elemento inverso :
Un número es inverso del otro si al multiplicarlos obtenemos como resultado el elemento unidad.
La suma de números naturales y de enteros no cumple esta propiedad.
Distributiva :
El producto de un número por una suma es igual a la suma de los productos de dicho número por cada uno de los sumandos.
a · (b + c) = a · b + a · c
Sacar factor común :
Es el proceso inverso a la propiedad distributiva.
Si varios sumandos tienen un factor común, podemos transformar la suma en producto extrayendo dicho factor.
a · b + a · c = a · (b + c) División
La división o cociente es una operación aritmética que consiste en averiguar cuántas veces un número está contenido en otro número.
D : d = c
Los términos que intervienen en un cociente se llaman, D, dividendo y d divisor. Al resultado, c, lo llamamos cociente.
Tipos de divisiones
División exacta :
Cuando el resto es cero.
D = d · c
División entera :
Cuando el resto es distinto de cero.
D = d · c + r
Propiedades de la división
No es Conmutativo :
a : b ≠ b : a
. Cero dividido entre cualquier número da cero.
0 : a = 0
No se puede dividir por 0.
Potenciación
La potenciación es una multiplicación de varios factores iguales.
a · a · a · ... = an
Base
Es el número que multiplicamos por sí mismo.
Exponente
Indica el número de veces que multiplicamos la base. Propiedades de la potencias
1. a 0 = 1
a 1 = a
Producto de potencias con la misma base :
Es otra potencia con la misma base y cuyo exponente es la suma de los exponentes.
am · a n = am+n
División de potencias con la misma base :
Es otra potencia con la misma base y cuyo exponente es la diferencia de los exponentes.
am : a n = am - n
25 : 22 = 25 - 2 = 23
Potencia de una potencia :
Es otra potencia con la misma base y cuyo exponente es el producto de los exponentes. (am ) n = am · n
Producto de potencias con el mismo exponente :
Es otra potencia con el mismo exponente y cuya base es el producto de las bases.
an · b n = ( a · b) n
Cociente de potencias con el mismo exponente:
Es otra potencia con el mismo exponente y cuya base es el cociente de las bases. an : bn = ( a : b) n
Radicación
Es la operación inversa a la potenciación. Y consiste en que dados dos números, llamados radicando e índice, hallar un tercero, llamado raíz, tal que, elevado al índice, sea igual al radicando.
En la raíz cuadrada el índice es 2, aunque en este caso no se pondría. Consistiría en hallar un número conocido su cuadrado.
La raíz cuadrada de un número, a, es exacta cuando encontramos un número, b, que elevado al cuadrado es igual al radicando: b2 = a.
Cuadrados perfectos
Son los números que poseen raíces cuadradas exactas. Raíz cuadrada exacta
Radicando = (Raíz exacta) 2 Raíz cuadrada entera
Radicando = (Raíz entera)2 + Resto Logaritmación
El logaritmo de un número, en una base dada, es el exponente al cual se debe elevar la base para obtener el número.
Propiedades de los logaritmos
No existe el logaritmo de un número con base negativa. No existe el logaritmo de un número negativo.
No existe el logaritmo de cero. El logaritmo de 1 es cero.
El logaritmo en base a de a es uno.
El logaritmo en base a de una potencia en base a es igual al exponente.
Logaritmo de un producto
El logaritmo de un producto es igual a la suma de los logaritmos de los factores.
Logaritmo de un cociente
El logaritmo de un cociente es igual al logaritmo del dividendo menos el logaritmo del divisor.
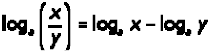
Logaritmo de una potencia
El logaritmo de una potencia es igual al producto del exponente por el logaritmo de la base.
Logaritmo de una raíz
El logaritmo de una raíz es igual al cociente entre el logaritmo del radicando y el índice de la raíz.
Resolución de problemas con operaciones básicas
Juan tiene 85 pesos y se ha comprado una chocolate que le costó 35 y unos caramelos que le costaron 25.
¿Cuánto dinero le sobrará?
25
15
30
20
Compré un bote de mermelada de 52 y una lata de sardinas de 36. Si pagué con un billete de 100.00. ,
¿Cuánto me devolvieron?
9
10
12
14
Tenía 95. Compré un balón de 68 y un chocolate de 24 ¿cuántas pesetas me sobraron?
4
2
1
3
Germán tiene 12 cromos y Luis tiene 17. ¿Cuántos tienen entre los dos?
29
30
19
28
Germán tiene 12 cromos y Luis tiene 17. ¿Cuántos cromos tiene Luis más que Germán?
5
4
6
3
En un cine hay 54 hombres, 74 mujeres y 12 niños. ¿Cuántas butacas se han ocupado si el cine tiene 300 butacas?
A) 200
B) 100
C) 140
D) 150
En un cine hay 54 hombres, 74 mujeres y 12 niños. ¿Cuántas butacas se han quedado libres si el cine tiene 300 butacas?
A) 200
B) 160
C) 150
D) 140
En el cuartel hay 426 soldados. Han llegado 318 soldados más y se han ido 26. ¿Cuántos hay ahora?
A) 718
B) 728
C) 708
D) 700
A una niña por su cumpleaños le regalan dinero, su padre le da 100
se compra un chocolate que le cuesta 65 , ¿cuánto le queda?
A) 140
B) 100
C) 130
D) 150
, su madre 50
, su abuela 65
. Si
En un vaso ponemos 0,12 litros de agua; en otro vaso 0,18 y en otro 0,17. ¿Cuánto hay entre los tres?
El padre de Juan entregó 10,75 euros a sus cinco hijos. ¿Cuánto le tocó a cada uno?
José Luis tenía 12,05 euros y gastó 3,25 en un bolígrafo. ¿Cuánto le queda?
Una bolsa de pipas vale 0,55 euros. ¿Cuánto costarán 7 bolsas?
Pedro tenía que recorrer 7,25 kilómetros y por la mañana hizo 3,3 km. ¿Cuánto le falta?
El tío de Andrés quiere repartir 14,52 euros entre sus tres sobrinos. ¿Cuánto dará a cada uno?
Un cuaderno vale 0,35 euros. ¿Cuánto costarán 6 cuadernos?
En una botella hay 1,45 litros y en otros 0,85 litros. ¿Cuánto hay entre las dos?
Un profesor reparte 21,85 euros entre los 19 alumnos de la clase. ¿Cuánto dará a cada uno?
Una caja contiene 120 manzanas. Si el peso medio de una manzana es de 75 g. ¿Cuántos kg pesarán todas las manzanas?
Una familia gasta 200 euros al día. ¿Cuánto gastará en una semana?
Un lápiz vale 0,15 euros. ¿Cuánto costarán 7 lápices?
¿Cuánto pagaré por dos pantalones y una camiseta si cada pantalón cuesta 30 euros y la camiseta 11 euros?
Un viajero da 12
asiento?
para pagar el billete de ferrocarril y le devuelven 2,40
. ¿Cuánto ha pagado por su
Un hombre compra un traje por 85
comerciante?
; da al comerciante dos billetes de 50
. ¿Qué suma le devolverá el
La longitud de un río es de 940 km y la de otro de 928 km. ¿Cuántos km tiene más el primero que el segundo?
Si mi hermano gemelo tiene 14 años ¿Cuántos años tenemos entre los dos?
Un padre tenía 29 años al nacer su hijo. ¿Cuál será la edad del hijo cuando el padre cumpla 68 años?
Un vaso vacío pesa 1789 gr; lleno, 9395 gr. ¿Cuánto pesa el contenido?
Los árabes invadieron España en el año 711 y fueron expulsados de ella en 1492. ¿Cuánto tiempo permanecieron en la península?
Una persona compra 5 kg de manteca a razón de 2,40 . El kg. ¿Cuánto le devolverán si entrega un billete de 20?
Una persona gana 15,25
diarias y gasta 8,10
. A diario ¿Cuánto será su dinero al cabo de 6 días?
Si mi sueldo es 2050 al mes ¿Cuánto ganaré al año?
Un contratista ocupa a 28 obreros de los que 9 ganan 120
¿Qué suma necesita para pagarles 12 días de trabajo?
de jornal, 12 reciben 10
y los demás 15 .
Un comerciante recibe cuatro pedidos de 495 botellas cada uno; habiendo efectuado dos envíos de 876 botellas cada uno, ¿cuántas botellas le quedan aún?
Un comerciante compra 45 docenas de platos al precio de 12 la docena; rompe 10 platos y vende los restantes a 1,20 cada uno. ¿Cuál es su ganancia?
Para pagar una deuda entrego dos billetes de 20 . Y uno de 10 ; me devuelven una moneda de 2 ,
dos de 1 , una de 20 céntimos y otra de 10 céntimos. ¿A cuánto ascendía mi deuda?
Vendiendo 13 sacos de grano a 25. Cada uno, se ganan 50 . Sobre el precio de compra. ¿Cuánto han costado los 13 sacos?
En una clase hay 30 alumnos. Las 3/5 partes son chicas ¿Cuántas chicas hay?
Si las 5/6 partes de los 120 alumnos de un colegio practican deporte ¿Cuántos practican deporte?
Clave
1.A 2.C 3.C 4.D 5.A 6.A 7.C 8.B 9.A 10.D 11. 0,47 12. 2,15 13. 8,8 14. 3,85 15. 3,95
16. 4,84 17. 2,1 18. 2,3 19. 1,15 20. 9 21. 1400 22. 1,05 23. 71 24. 9,6 25. 15 26. 12 27. 28
28. 39 29. 7606 30. 781 31. 8 32. 42,9 33. 24600 34. 1305 35. 228 36. 96 37. 45,7 38. 275
39. 18 40. 100
Examen creado con That Quiz — el sitio para crear exámenes de matemáticas.
Link: https://www.thatquiz.org/es/previewtest?E/I/R/L/02561239548214
Operaciones combinadas
Al resolver problemas y ejercicios en que se combinan adiciones, sustracciones, multiplicaciones y divisiones, es necesario seguir el siguiente orden:
1° Multiplicaciones y divisiones, de izquierda a derecha. 2° Adiciones y sustracciones, de izquierda a derecha.
Resuelve los siguientes ejercicios con la calculadora, utilizando el orden de las operaciones mencionado.
a) 2 560 x 11 + 2 900 - 1500
b) 8 966 : 2 - 345 x 2
c) 121 453 x 3 - 870 : 5
d) 45 000 : 15 + 123 x 12
Al resolver ejercicios combinados en los cuales hay paréntesis, primero se debe resolver lo que hay dentro de cada paréntesis. Por ejemplo:
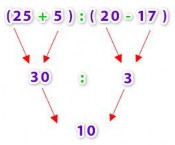
En resumen para calcular una serie de operaciones combinadas se siguen los siguientes pasos:
Primero, se calculan las operaciones que tienen paréntesis.
Luego, se calculan las multiplicaciones y divisiones de izquierda a derecha.
Por último, se calculan las sumas y las restas de izquierda a derecha.
Resuelve los siguientes ejercicios combinados, resolviendo primero los paréntesis.
a) ( 45 + 38 ) x ( 48 - 12 )
b) 3 x ( 20 x 5 - 4 x 12 )
c) ( 230 000 - 150 000) : 2
d) ( 90 + 1 600 ) x 7
¿Hay alguna diferencia en los resultados de los ejercicios anteriores? ¿Por qué?
Ana compró 5 revistas a $ 2 500 cada una y 5 paquetes de galletas a $ 300 cada uno. ¿Cuál de los ejercicios anteriores le permite saber el precio total de su compra?
Resuelve los siguientes problemas
Felipe colecciona estampillas. Las guardas en un álbum que tiene 14 páginas. Cada página tiene 2 filas con 8 espacios cada una. Si completa su álbum, ¿cuántas estampillas tiene en él?
A Macarena le encantan los aros. Si los guarda en 4 cajas y en cada una tiene 8 pares y en una de ellas tiene además un solo aro. ¿Cuántos pares de aros tiene en total Macarena?
Javiera plantó 7 bulbos de tulipanes y 2 de lilium. Si salen 5 tulipanes de cada bulbo, ¿Cuántos tulipanes florecerán en el jardín de Javier?
Chile es uno de los dos paises del mundo que producen lapislásuli. Esta piedra se exporta generalmente en forma elaborada, como joyas o elementos de ornamentación. Un joyero logra hacer 32 collares de lapislásuli en una semana, los cuales empaca en cajas donde caben 4. ¿Cuántas cajas necesitará para empacar los 32 collares?
Un joyero coloca 30 collares en una vitrina. Si los separa en grupos de 6 collares cada uno, ¿Cuántos grupos de collares podrá formar?
Entro otros productos que Chile exporta está el vino. Estos son enviados en cajas que evitan los golpes y van muy resguardados, incluso se envían en presentaciones de lujo, combinando tipos de vino. Si hay 52 botellas de vino y se embalan de dos en cada caja ¿Cuántas cajas de vino se podrán armar?
Respuestas
2.1- 224 estampillas
2.2- 32 pares y sobra 1
2.3- 35 tulipanes
2.4- 8 cajas
2.5- 5 grupos
2.6- 26 cajas
NÚMEROS FRACCIONARIOS Y DECIMALES
Relaciones de proporcionalidad directa e inversa
Proporción
Una proporción es la igualdad de dos razones.
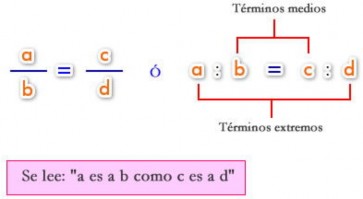
Propiedad fundamental
En toda proporción, el producto de los términos medios es igual al producto de los términos extremos (Teorema fundamental de las proporciones). Es decir:
Ejemplo: Si tenemos la proporción:
Y le aplicamos la propiedad fundamental señalada queda: 3 • 20 = 4 • 15, es decir, 60 = 60.
Esta es la propiedad que nos permite detectar si dos cantidades presentadas como proporción lo son verdaderamente.
Proporcionalidad directa
Dos variables (una independiente x y la otra dependiente y) son directamente proporcionales si el cociente (división) entre los valores respectivos de cada una de las variables es constante.
y / x = k
Además, al aumentar o disminuir una de ellas, la otra aumenta o disminuye, respectivamente, en la misma razón.
Ejemplo:
- Indica si las variables son directamente proporcionales
La medida del lado de un cuadrado y su perímetro: b.
Respuesta Sí, porque a mayor longitud de sus lados mayor perímetro. (si una variable aumenta la otra aumenta en la misma razón).
c. El número de trabajadores y los días que se demoran en hacer un trabajo, si todos trabajan de igual manera: Respuesta: No, porque a mayor cantidad de trabajadores menos cantidad de días. (si una variable aumenta, la otra disminuye en la misma razón).
En el caso de las funciones esta proporcionalidad directa se puede representar como una función de la forma
y = k x Dónde:
y : variable dependiente. x: variable independiente.
k : constante de proporcionalidad.
Por ejemplo: si tenemos la siguiente función: y = 3 x
La constante de proporcionalidad sería 3.
¿Cómo se calcula la constante de proporcionalidad?
Como y = k x entonces: k = y / x
Calcula la constante de proporcionalidad: | |||
x | 3 | 6 | 7 |
y | 6 | 12 | 14 |
k = 6 / 3
k = 2
El cociente de las dos magnitudes es siempre el mismo (constante)
Gráfico de proporcionalidad directa
El gráfico correspondiente a una relación de proporcionalidad directa es una línea recta que pasa por el punto de origen de un sistema de coordenadas cartesianas.
En una función de prorcionalidad directa, si una de las variables aumenta, la otra también aumenta en un mismo factor; y si una de las variables disminuye, la otra disminuye en un mismo factor.
Ejemplo:
Juan ha utilizado 20 huevos para hacer 4 tortillas iguales. ¿Cuántos huevos necesita para hacer 6 tortillas? ¿Y para hacer 2?
Grafica los resultados hasta 6 tortillas.
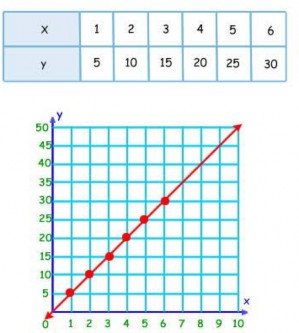
Como puedes ver, el gráfico es una línea recta que pasa por el origen. Además, si nos fijamos en la tabla, nos podemos dar cuenta que el cociente (división) entre las dos magnitudes (y / x) es constante. En este caso el valor de la constante de proporcionalidad es 5.
Proporcionalidad inversa
Dos variables (una independiente x y la otra dependiente y) son inversamente proporcionales si el producto entre los valores respectivos de cada una de las variables es constante.
( x • y = k )
Además, en una función de proporcionalidad inversa, si una de las variables aumenta, la otra disminuye en un mismo factor; y si una de las variables disminuye, la otra aumenta en un mismo factor.
Esta relación de proporcionalidad inversa se puede representar como una función de la forma:
y = k / x
Dónde:
y : variable dependiente. x: variable independiente.
k : constante de proporcionalidad.
Ejemplos:
Indica si las variables son inversamente proporcionales.
El número de albañiles y el tiempo empleado en hacer el mismo edificio.
Respuesta: Son inversamente proporcionales, ya que, con el doble, triple... número de albañiles se tardará la mitad, tercera parte de tiempo en construir el mismo edificio.
La velocidad de un auto y el trayecto recorrido en el mismo tiempo.
Respuesta: No es inversa ya que, a tiempo constante, con el doble o el triple... de la velocidad, el auto recorrerá el doble, triple... de espacio.
La velocidad de un auto y el tiempo empleado en recorrer el mismo trayecto.
Respuesta: Son inversamente proporcionales, ya que, a espacio constante, con el doble, triple... velocidad, el auto tardará la mitad, tercera parte... de tiempo en recorrerlo.
2.2- Gráfico de proporcionalidad inversa
La representación gráfica de esta función son puntos que pertenecen a una curva, llamada hipérbola.
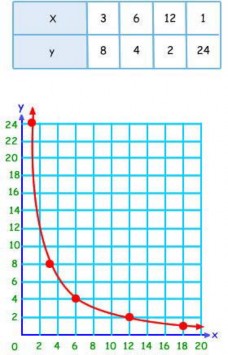
Resumen: Observa el siguiente cuadro comparativo:
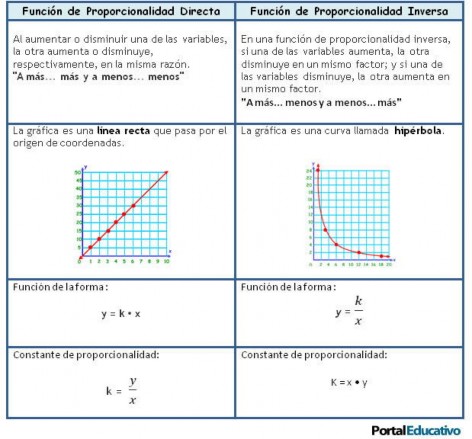
Preguntas:
Si 5 m de género valen $8500, ¿cuánto valen 8 m? R: valen $13600
Veinte alumnos hicieron una excursión y consumieron 15 botellas de jugo. ¿Cuántas botellas de jugo se habrían consumido, si hubieran ido los 50 alumnos del curso? R: 38 botellas
A cierta hora de un día asoleado, una persona, de 1,75 m de altura, proyecta una sombra de 1,25 m de longitud. Calcula la altura de un árbol del lugar que, en el mismo momento, tiene una sombra de 12 m de largo. R: 16,8 metros
Una piscina con un largo de 12cm y un ancho de 4cm., dibujada en un plano. Si en la realidad el largo es 36m, ¿cuál es el ancho? R: 12 metros
Rosa pesa 48 kilos y José pesa 52 kilos. Dividir una barra de chocolate de 200 gramos en la misma razón que sus pesos. R: 96 y 104 gramos
Con el dinero que tengo, puedo comprar 20 chocolates a $ 20 cada uno. Si los chocolates suben a $ 25,
¿cuántos podré comprar? R: puede comprar 16 chocolates
Si 25 telares producen cierta cantidad de tela en 60 horas, ¿cuántas horas emplearán 42 telares iguales en producir la misma cantidad de tela? R: 35 horas, 42 minutos y 52 segundos
Dos ruedas dentadas están engranadas. La primera tiene 12 dientes y la segunda 28. ¿Cuántas vueltas habrá dado la segunda, cuando la primera ha dado 84 vueltas? R: 36 vueltas.
Significado y uso de las operaciones básicas con números fraccionales y decimales.
Suma y resta de números decimales
Se colocan en columna haciendo corresponder las comas.
Se suman (o se restan) unidades con unidades, décimas con décimas, centésimas con centésimas…
342.528 + 6 726.34 + 5.3026 + 0.37 =
372.528 – 69.68452 =
Multiplicación de números decimales
Se multiplican como si fueran números enteros.
El resultado final es un número decimal que tiene una cantidad de decimales igual a la suma del número de decimales de los dos factores.
46.562 · 38.6
Multiplicación por la unidad seguida de ceros
Para multiplicar un número por la unidad seguida de ceros, se desplaza la coma hacia la derecha tantos lugares como ceros acompañen a la unidad.
División de números decimales Sólo el dividendo es decimal
Se efectúa la división como si de números enteros se tratara. Cuando bajemos la primera cifra decimal, ponemos una coma en el cociente y continuamos dividiendo.
526.6562: 7 =
Sólo el divisor es decimal
Quitamos la coma del divisor y añadimos al dividendo tantos ceros como cifras decimales tiene el divisor. A continuación, dividimos como si fueran números enteros.
5126: 62.37 =
El dividendo y el divisor son decimales
Se iguala el número de cifras decimales del dividendo y el divisor, añadiendo a aquel que tuviere menos, tantos ceros como cifras decimales de diferencia hubiese. A continuación, se prescinde de la coma, y dividimos como si fueran números enteros.
5627.64: 67.5261
División por la unidad seguida de ceros
Para dividir un número por la unidad seguida de ceros, se desplaza la coma hacia la izquierda tantos lugares como ceros acompañen a la unidad.
Una fracción es un número que se obtiene dividiendo un número por otro. Suele escribirse en la forma 
o ½ o 1 / 2. En una fracción tal como a/b el número a que es dividido se llama numerador y el número b que divide, divisor o denominador.
Cuando una fracción se escribe en la forma 2 / 3 el numerador queda arriba y el denominador abajo. Las fracciones pueden clasificarse de la siguiente manera:
Fracción propia: en la que el numerador es menor que el denominador; por ejemplo, 
o ⅔. Las fracciones propias son las que mejor responden a la denominación de fracción, ya que son parte de la unidad. También se llaman fracciones simples.
Fracción impropia: en las que el numerador es mayor que el denominador; por ejemplo., 4/3, 8/7, 206/3, 4/1 etc. Si la fracción se escribe como un número entero seguido de una fracción simple -por ejemplo 1 1/3 en vez de 4/3- se trata de una fracción mixta.
Fracción decimal: hablando con propiedad, un decimal es cualquier número escrito en notación decimal (esto es, en base diez). No obstante, el término suele utilizarse para designar una fracción decimal, o fracción escrita utilizando el sistema de notación posicional decimal. Lo mismo que para formar grupos en los números enteros se utilizan decenas, cientos, miles, etc., para formarlos en las fracciones decimales se recurre a décimas, centésimas, milésimas, etc. Así, un decimal como 0,05 es igual a 5 centésimas (5/100) y así sucesivamente.
Un número como 127,836 es una fracción decimal mixta que se representa:
(1×100) + (2×10) + (7×1) + (8×1/10) + (3×1/100) + (6×1/1000).
Ello equivale a escribir el número como suma de potencias decrecientes de diez (obsérvese que 100=1) (1×102) + (2×101) + (7×100) + (8×10-1) + (3×10-2)+(6×10-3).
Un decimal puede tener un número finito de dígitos (por ejemplo, 5/8 es igual a 0,625); tales decimales se llaman exactos. También puede ocurrir que el decimal prosiga indefinidamente, esto es, que contenga un número infinito de dígitos; se los llama decimal no exacto.
Fracción ordinaria: Una fracción ordinaria es el cociente entre dos números. El número que es dividido se llama numerador y el que divide denominador. Si a y b son dos números, entonces la fracción que representa el cociente de a por b se escribe a/b. El concepto de fracción puede ilustrarse (principalmente en casos simples como los de 1/2, 2/3 o 3/4) por medio de círculos y cuadrados.
Como una fracción es una cantidad dividida por otra, su valor no cambia si el numerador y el denominador son multiplicados por un factor común. Si ambos se dividen por su MCD, la fracción ya no puede simplificarse más.
Porcentajes
Porcentaje quiere decir partes por 100
Cuando dices “por ciento” en realidad dices “por cada 100”
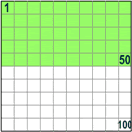
Así que 50% quiere decir 50 por 100 (50% de la caja es verde)
Y 25% quiere decir 25 por 100 (25% de la caja es verde)
Ejemplos: Porcentajes de 80
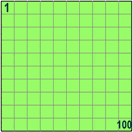
100% of 80 is 100/100 × 80 = 80
So 100% means all.
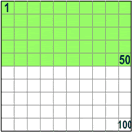
50% of 80 is 50/100 × 80 = 40
So 50% means half.
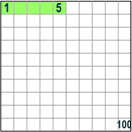
5% of 80 is 5/100 × 80 = 4
So 5% means 5/100ths.
Usando Porcentajes
Como “por ciento” quiere decir “por cada 100” deberías pensar siempre que “hay que dividir por 100” Así que 75% quiere decir 75/100
Y 100% es 100/100, o exactamente 1 (100% de cualquier número es el mismo número)
Y 200% es 200/100, o exactamente 2 (200% de cualquier número es el doble del número) Un porcentaje también se puede escribir como un decimal o una fracción.
La mitad se puede escribir…
Como porcentaje: 50%
Como decimal: 0.5
Como fracción: 1/2
Ejemplos
Calcula 25% de 80
25% = 25/100 
(25/100) × 80 = 20
Así que 25% de 80 es 20
Un Skateboard tiene una rebaja de 25%. El precio normal es
$120. Calcula el nuevo precio
Calcula 25% de $120
25% = 25/100 
(25/100) × $120 = $30
25% de $120 es $30
Así que la reducción es $30
Quita la reducción del precio original
$120 – $30 = $90
El precio del Skateboard en rebajas es $90
Link: https://matematicasconalepvallarta.wordpress.com/category/habilidad-matematica/1-significado- y-uso-de-los-numeros/1-3-numeros-fraccionarios-y-decimales/
Potenciación y Radicación
Potenciación
Es la operación aritmética que tiene por objeto multiplicar por sí mismo un número llamado base tantas veces como indica otro número llamado exponente.
Si escribimos 53, 5 será la base y 3 será el exponente, con lo cual tendremos que: 
Cuando el exponente es 2, o sea, cuando estamos hallando la segunda potencia de la base, se acostumbra decir que estamos hallando el cuadrado de la base. Por ejemplo 
. El término cuadrado viene de la nomenclatura geométrica, puesto que el cuadrado de un número equivale en las unidades correspondientes de superficie al área de un cuadrado. El área de un cuadrado con un lado de 5m. Será 
m2.
Cuando el exponente es 3, es cuando estamos hallando la tercera potencia de la base se acostumbra decir que estamos hallando el cubo de la base. 
, es el resultado de hallar el cubo de 5. El término cubo también viene de la nomenclatura geométrica, ya que el cubo de un número equivale en unidades correspondientes de volumen al volumen del cubo cuya arista es dicho número.
Cuando los exponentes son 4, 5, 6, 7, 8, etc. se dice que estamos elevando la base a la cuarta, quinta, sexta, séptima u octava potencia, respectivamente:
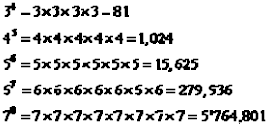
La potencia enésima de un número a equivaldrá a multiplicar n veces a por sí mismo: 
veces.
Ley de uniformidad
Cualquier potencia de un número tiene un valor único o siempre igual.
E J E M P L O
22=4 Siempre 53=125 Siempre
Potencia de un producto
Para elevar un producto a una potencia se eleva cada uno de los factores a dicha potencia y se multiplican esas potencias.
Si tenemos el producto abc, Vamos a probar que (abc)n=an·bn·cn
Elevar el producto abc a la enésima potencia equivale a tomar este producto como factor n veces; luego:
Esta propiedad constituye la ley distributiva de la potenciación respecto de la multiplicación.
E J E M P L O
Resolver (3×4×5)2 SOLUCIÓN: (3×4×5)2 = 32·42·52 = 9×16×25 = 3600
Potencia de un número fraccionario
Para elevar un cociente exacto o una fracción a una potencia cualquiera se elevan su numerador y denominador a dicha potencia.
Si tenemos la fracción 
; Según la definición de potencia elevar 
a la potencia n será tomarlo como factor n veces; luego:
Esta propiedad constituye la ley distributiva de la potenciación respecto de la división exacta.
E J E M P L O
Elevar 
SOLUCIÓN: 
E J E M P L O
Elevar SOLUCIÓN:
E J E M P L O
Desarrollar 
SOLUCIÓN:
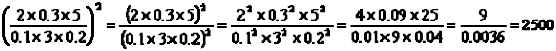
E J E M P L O
Desarrollar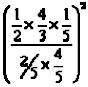 
SOLUCIÓN:
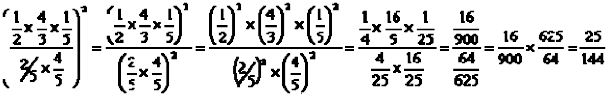
E J E M P L O
Desarrollar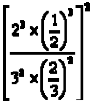 
SOLUCIÓN:
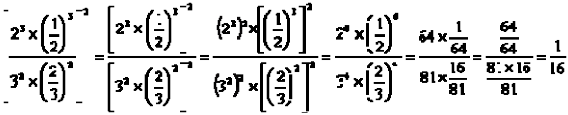
Algebra
Significado y uso de las literales
Una ecuación es una igualdad, es decir, que los dos miembros separados por el signo = son iguales. Hay una situación de equilibrio entre los términos de cada miembro, que debes considerar cuando quieras resolver una ecuación.
Cuando planteas una ecuación, es importante que reconozca que hay algo desconocido que puede ser determinado considerando las restricciones del problema. Lo que desconoces lo puedes representar con cualquier literal y representa la incógnita del problema.
Conforme resuelves las operaciones indicadas en la ecuación, obtendrás ecuaciones equivalentes y cada vez mas reducidas hasta obtener el valor de la incógnita.
Para resolver una ecuación de primer grado que tiene una incógnita se siguen los pasos descritos a continuación.
Ecuaciones de la forma
ax + b = c
Ejemplo
Resolver la ecuación:
Paso 1:
Paso 2:
Paso 3:
3x – 8 + 8 = 7 + 8
3x = 15
x=15/3
RESULTADO ES = X=5
COMPROBACIÒN:
3X – 8 = 7
3 (5) – 8 = 7
15 – 8 = 7
7 = 7
Link: http://compumateizquierdo.blogspot.mx/2011/03/significado-y-uso-de-las-literales.html
Ecuaciones
Término algebraico consta de:
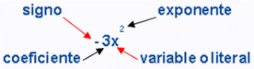
Expresiones algebraicas y reducción de términos semejantes.
Una expresión algebraica es una combinación de letras y números ligadas por los signos de las operaciones: adición, sustracción, multiplicación, división y potenciación.
—El doble o duplo de un número: 2x
—El triple de un número: 3x
—El cuádruplo de un número: 4x
—Un tercio de un número: x/3.
—Un número al cuadrado: x2
—Un número al cubo: x3 Términos Semejantes:
Los términos son semejantes cuando tienen el mismo factor literal.
Los T. S. se pueden sumar o restar, sumando o restando sus coeficientes numéricos y conservando el factor literal.
Ejemplo:
El término 3x2y y el término 2x2y , son semejantes. (Tiene factor literal iguales) y al sumarlo da 5x2y. 3x2y + 2x2y = 5x2y.
Ejemplos aplicados:
Obtén el perímetro con los datos representados. a= 10 cm
2a
P= 2a + 2a + 2a +2a = 8a = 8(10)= 60 cm.
2a
6a
P= 6ª + 2ª + 6ª + 2 a = 16ª= 16(10) = 160 cm
Ejercicios
Resuelve: Calcula el perímetro de las siguientes figuras.
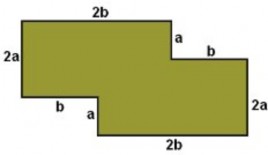
Link: http://rogermatematiks.blogspot.mx/2011/06/significado-y-uso-de-las-literales-2do.html
Expressions Algebraicas
Expresión común de problemas algebraicos de adicción y sustracción
Una expresión algebraica es una combinación de números y letras relacionados mediante operaciones aritméticas; adición, sustracción, multiplicación, división y potenciación. La expresión algebraica está conformada por TÉRMINOS.
En Matemáticas es frecuente utilizar expresiones que combinan números y letras o solamente letras. Las expresiones que resultan de combinar números y letras, relacionándolos con las operaciones habituales se llaman expresiones algebraicas.
EXPRESIÓN ALGEBRAICA: Una expresión algebraica es una combinación de números y letras relacionados mediante operaciones aritméticas. Adición, sustracción, multiplicación, división y potenciación.
La expresión algebraica está conformada por TÉRMINOS
Ejemplo, la siguiente expresión Algebraica está conformada por tres términos: (3y), (-2xy), (8)
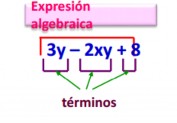
UN TÉRMINO es una expresión algebraica que consta de un solo símbolo o de varios símbolos separados únicamente por la multiplicación o la división. Aquí no hay sumas ni restas para separarlos.
GRADO ABSOLUTO DE UN TÉRMINO: Se denomina grado absoluto de un término algebraico a la suma de los exponentes de su factores literales: 3x 3, este término es de grado tres -5x2y 3, es de grado 5, porque la suma de los exponentes de sus factores literales es 2 + 3 = 5 • GRADO RELATIVO: Está dado por el exponente de la variable considerada (con relación a una letra). -5x2y 3: Es de 2º grado con respecto a la variable x -5x2y 3: Es de 3er grado con respecto a la variable y
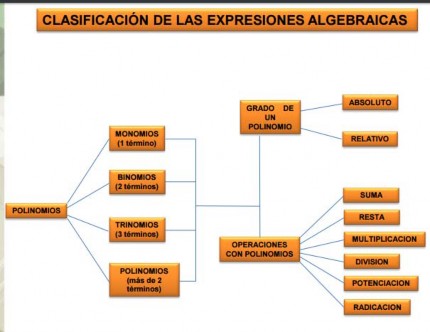
Monomio
Los monomios son polinomios que constan de un solo término. Ejemplos: 1) 7xy 2) –0,5xy 3) 4ab 4) -5xyz 5) 52abc 6) 3xz Debes tener en cuenta que en un monomio hay: 1. un factor numérico que se llama coeficiente, que en los ejemplos anteriores serían: 7 ,-0.5, 4 ,-5, 52, 3 respectivamente, 2. Una parte constituida por letras y sus exponentes que se llama parte literal, como son xy, xy , ab, xyz para nuestros ejemplos anteriores. Los monomios que tienen la misma parte literal se llaman monomios semejantes, o simplemente términos semejantes, como son: 5xy2 , -7xy2 , 3xy2 .
Polinomio
Un Polinomio es una expresión algebraica que consta de dos o más términos algebraicos: Ejemplos: 1) -7x2 + 4x – 5xy 3) 5a2 + 3ab - ab2 - 2 2) 6x4 - 5x3 + x2 + 4x + 9 4) 6x3 + 2x2 – x +1 De acuerdo a la cantidad de sumandos el polinomio recibe denominaciones particulares como: Binomio y Trinomio:
Binomio
Binomio: es un Polinomio que consta de dos términos. Ejemplos: 1) 5x2y + 2x2y 3 3) 4a2b + 4a3b 3 5) 8m3n 2
- 2mn2 2) -4x + 3y 4) 6x2y 2z - 3xy 6) – 4x -2xy
Trinomio
Trinomio: es un Polinomio que consta de tres términos. Ejemplos: 1) 5x + 6y + 3z 3) 4mn2 + 2m2n – 3mn 5) a2+b2 + 3ab3 + ab 2) –1 + ab + 3a2b 4) -3xy2z + 3x2y 2z +x2y2z 3 6) x 3y 2 + xy2 +3xy
Grado de un polinomio
El grado de un polinomio está determinado por el término de mayor grado absoluto. Ejemplo: 2x 3y + 5xy2 - x z + 1 es de grado 4, OBSERVA: el término 2x 3y que es de grado 4. El grado de un polinomio respecto de una variable es el mayor exponente con que figura dicha variable. Así en el ejemplo anterior es de grado 3 respecto de x, de grado 2 respecto de y, de grado 1 respecto de z.
Resolución de problemas con expresiones
EL LENGUAJE ALGEBRAICO
Utilizando el lenguaje algebraico se puede expresar simbólicamente diversas generalizaciones y resolver diferentes situaciones de la vida cotidiana: En estos casos las letras funcionan como representaciones de relaciones aritmética y de situaciones reales en problemas concretos.
Así es posible representar diferentes enunciados por medio de expresiones algebraicas o interpretarlas para transformarlas en enunciados que representen algún tipo de situación. Expresiones verbales tales como “el doble”, “el triple”, “la mitad”, “la cuarta parte” se pueden expresar en forma algebraica. Por ejemplo
Lenguaje Verbal | Lenguaje algebraico |
Un número determinado | x |
El doble de un numero | 2x |
La mitad de un numero | x/2 |
Las tres cuartas partes de un numero | 3x/4 |
El triple de un numero aumentado en cinco | 3x + 5 |
La tercera parte de un número disminuido en siete | x/3 – 7 |
La cuarta parte del cuadrado de un numero | X2/4 |
Tres números consecutivos | X, x +1 , x + 2 |
El cubo de un numero disminuido en sus dos terceras partes | X3 - 2x/3 |
PLANTEAMIENTO Y RESOLUCION DE PROBLEMAS
Para solucionar problemas relacionado con el planteamiento de ecuaciones, es conveniente tener en cuenta los siguientes pasos.
Interpretación del enunciado. Al leer el enunciado se debe identificar la incógnita del problema expresando la información necesaria en término de dicha incógnita.
Planteamiento y resolución de la ecuación. con la información necesaria en término de la incógnita, se plantea la ecuación que relaciona los datos del problema. Luego, se resuelve la ecuación planteada conforme a los criterios, pasos y procedimientos de resolución de ecuación estable cedido anteriormente.
Comprobación de la solución. Se verifica la solución hallada, comprobando que cumple con las condiciones del enunciado del problema
EJERCICIO RESUELTO
Carolina compro un esfero, un lápiz y un borrador por $1.900, el esfero costo el triple de lo que costo el borrador y el lápiz $200 menos que el esfero. ¿Cuánto costo cada artículo?
SOLUCION
Interpretación del enunciado
Se asigna la incógnita al costo del borrador y se expresa el costo de los demás artículos en función de dicha incógnita. Así,
Borrador: x esfero: 3x lápiz: 3x -200
Planteamiento y solución de la ecuación
El costo de los tres artículos es de $ 1.900. Así, X + 3x + (3x -200) = 1.900
X + 3x + 3x – 200 = 1.900
X + 3x +3x = 1900 + 200
7x = 2.100 X = 2.100/7 X = 300
Al remplazar el valor de la incógnita en cada uno de los datos del problema, se tiene que, Borrador: 300
Esfero: 3(300) = 900
Lápiz: 3(300) – 200 = 700
Luego, el costo del borrador es de $300, el del esfero $ 900 y el del Lápiz es $700
Comprobación de la solución
La suma de los valores los tres artículos es $300 + $900 +$700 = $1.900
Para elegir el personero de un colegio, se realizó una votación en la cual se registró un total de 560 votos. Miguel obtuvo 75 votos menos que Camilo y 55 votos más que Leonardo. ¿Cuantos votos obtuvo cada candidato?
SOLUCION
Interpretación del Enunciado
Se asigna la incógnita al número de votos obtenidos por Miguel y se expresa el número de votos De los demás candidatos en función de dicha incógnita. Así.
Número de votos para Miguel: X Número de Votos para camilo: x +75 Número de votos para Leonardo: x – 55
Planteamiento y resolución de la ecuación El total de Voto fue de 560. Así
X + (x + 75) + (x -55) = 560 X + x + 75 + x – 55 =560
X + x + x = 560 – 75 + 55 se hizo transposición de términos semejantes 3x= 540 se hizo reducción de términos semejantes
X = 540/3 Se despejo x
X = 180 se realizó la división
Al remplazar el valor de la incógnita en cada uno de los datos del problema se tiene que, Número de votos para Miguel: 180
Número de Votos para camilo: 180 +75 = 255 Número de votos para Leonardo: 180 – 55 = 125
Luego miguel obtuvo 180 votos, camilo 255 y Leonardo 125
Comprobación de la solución
La suma de los votos de los tres candidatos es 180 + 225 + 125 = 560, los cuales satisface las condiciones del problema
PROBLEMAS PROPUESTOS
La edad de un padre es el triple de la edad de su hijo, la edad que tenía el padre hace 7 años, era el doble de la edad que tendrá su hijo dentro de 6 años. ¿Qué edad tienen padre e hijo?
La edad de luna es cuatro veces la edad de estrella, si ambas edades suman 75 años. ¿Qué edad tiene cada una?
La suma de los ángulos de un triángulo es 180 grados. Si la medida del mayor es 6 veces la del menor y la de menor es 80 gados más que tercer Angulo ¿Cuánto mide cada Angulo?
La longitud de un rectángulo es 3m más que el doble del ancho. Si su perímetro es 72m, hallar las dimensiones
Un padre coloca 16 problemas a su hijo con la condición de que por cada problema que resuelva le da $12 y por cada problema que no resuelva le quita $5, si al final recibe $ 73. ¿Cuántos problemas resolvió?
La suma de las edades de un padre y su hijo es 50años. Si en cinco años el padre tendrá el doble de la edad de su hijo. ¿Qué edad tiene el hijo actualmente?
Un carpintero corto una tabla de madera de 140 cm en tres pedazos, el primer pedazo es 8cm más largo que el doble de la longitud del segundo pedazo y el tercer pedazo tiene tres veces la longitud del segundo pedazo. Encontrar la longitud de cada pedazo.
Link: http://matematicos3456.blogspot.mx/2012/08/planteamiento-y-resolucion-de-problemas.html
Ecuaciones de Primer Grado
Resolución de ecuaciones de primer grado
Concepto de ecuación
Para que exista una ecuación tiene que haber algo igual a algo. Una ecuación es de primer grado cuando la x (la variable) está elevada a uno.
Pasos para resolver una ecuación de primer grado
Si hay denominadores, los reducimos a común denominador (calculando el m.c.m) y suprimimos los denominadores.
Quitamos los paréntesis aplicando la regla de los signos. Al final tendremos a ambos lados del igual, sólo sumas y restas, unos términos llevaran x y otros no.
Trasposición de términos: Pasamos todos los términos con x a un lado de la ecuación, los números al otro lado.
Agrupamos los términos semejantes y al final despejamos la x obteniendo la solución.
Comprobamos la solución sustituyendo el valor de la x obtenida en la ecuación. Nos tiene que dar el mismo resultado a ambos lados de la ecuación.
Soluciones de una ecuación de primer grado. Ejemplos
Un número real: es cuando normalmente decimos que nos da solución. x + 3 = 5 x + 11 ⇒ x - 5 x = 11 - 3 ⇒ - 4 x = 8 ⇒ x = 8 / - 4 ⇒ x = - 2
Todo número real: nos da ⇒ 0 x = 0. Tiene solución para cualquier valor de x, decimos que tiene infinitas soluciones.
13 - 3 x - 9 = 8 x + 4 - 11 x ⇒ - 3 x - 8 x + 11 x = 4 + 9 - 13 ⇒ 0 = 0
Incompatible: se anulan las x y nos da ⇒ 0 x = número. No tiene solución. 6 + 5 x + 2 = 4 x - 2 + x ⇒ 5 x - 4 x - x = - 2 - 6 - 2 ⇒ 0 x = - 10
Link: http://www.vadenumeros.es/tercero/ecuaciones-de-primer-grado.htm
Resolución de problemas con ecuaciones de primer grado
Link: http://www.vadenumeros.es/tercero/problemas-primer-grado.htm
45 Problemas Resueltos de Ecuaciones de Primer Grado
Link: https://www.matesfacil.com/ESO/Ecuaciones/resueltos-problemas-ecuaciones.html
Sistemas de ecuaciones lineales de dos ecuaciones con dos incógnitas
Resolución de sistemas lineales de dos ecuaciones con dos incógnitas Link: http://www.vadenumeros.es/tercero/sistemas-de-ecuaciones.htm
Resolución de problemas con sistemas de dos ecuaciones lineales con dos incógnitas Link: http://www.vitutor.com/ecuaciones/sistemas/sistemas_ecuaciones.html
Link: http://www.vadenumeros.es/tercero/sistemas-de-ecuaciones.htm
Link: Ejercicios https://www.matesfacil.com/ESO/Ecuaciones/resueltos-problemas-sistema.html
Ecuaciones de segundo grado
Productos notables y factorización
Son aquellos productos que se rigen por reglas fijas y cuyo resultado puede hallarse por simple inspección. Su denominados también "Identidades Algebraicas". Son aquellos productos cuyo desarrollo es clásico y por esto se le reconoce fácilmente. Las más importantes son:
Binomio de Suma al Cuadrado: El Cuadrado del primer Término, más el Doble Producto del Primer por el segundo Término, más el Cuadrado del Segundo Término.
(a + b)2 = a2 + 2ab + b2
Binomio Diferencia al Cuadrado: El Cuadrado del primer Término, menos el Doble Producto del Primer por el segundo Término, más el Cuadrado del Segundo Término.
(a - b)2 = a2 - 2ab + b2
Diferencia de Cuadrados: El Cuadrado del Primer Término menos El Cuadrado del Segundo Término.
(a + b) (a - b) = a2 - b2
Producto de dos binomios que tienen un término común: El cuadrado del termino común, más el producto de termino común por la suma de los términos no comunes, más el producto de los términos no comunes.
(x + a)(x + b) = x2 + (a + b) x + ab
Binomio Suma al Cubo: El Cubo del Primer Término, más el triple producto del cuadrado del primer por el segundo Término, más el triple producto del primer por el cuadrado del segundo Término, más el cubo del segundo Término.
(a + b) 3 = a3 + 3 a2b + 3 ab2 + b3 = a3 + b3 + 3 ab (a + b)
Binomio Diferencia al Cubo El Cubo del Primer Término, menos el triple producto del cuadrado del primer por el segundo Término, más el triple producto del primer por el cuadrado del segundo Término, menos el cubo del segundo Término.
(a - b)3 = a3 - 3 a2b + 3 ab2 - b3
Suma de dos Cubos: Se saca raíz cubica a cada uno de los dos términos cúbicos, para obtener un binomio (la suma de dos números), y en base a ese binomio, se utiliza la siguiente regla para obtener un trinomio: el cuadrado del primero, menos el producto del primero por el segundo, más el cuadrado del segundo.
a3 + b3 = (a + b) (a2 – ab + b2)
Diferencia de Cubos Se saca raíz cubica a cada uno de los dos términos cúbicos, para obtener un binomio (la diferencia de dos números), y en base a ese binomio, se utiliza la siguiente regla para obtener un trinomio: el cuadrado del primero, más el producto del primero por el segundo, más el cuadrado del segundo.
a3 - b3 = (a - b) (a2 + ab + b2)
Trinomio Suma al Cuadrado ó Cuadrado de un Trinomio: El cuadrado del primer término, más el cuadrado del segundo término, más el cuadrado del tercer término, más el doble producto del primero por el segundo, más el doble producto del segundo por el tercero, más el doble producto del tercero por el primero.
(a + b + c) 2 = a2 + b2 + c2 + 2ab + 2bc + 2ac = a2 + b2 + c2 + 2 (ab + bc + ac)
Trinomio Suma al Cubo
(a + b + c)3 = a3 + b3 + c + 3(a + b). (b +c) (a + c)
Identidades de Legendre
(a + b)2 + (a – b)2 = 2 a2 2b2 = 2(a2 + b2)
(a + b) 2 + (a – b) 2 = 4 ab
Link: http://matematicas.obolog.es/productos-notables-factorizacion-4572
Resolución de ecuaciones de segundo grado
La ecuación 
parece complicada; pero en realidad es una ecuación de primer grado con una variable, ya que se puede transformar en esta ecuación equivalente: 7x-18=0
Hemos resuelto muchas ecuaciones de este tipo y hemos visto que siempre tienen una solución. Desde el punto de vista matemático, hemos resuelto esencialmente el problema de solucionar ecuaciones de primer grado con una variable.
En este apartado consideraremos el siguiente tipo de ecuaciones polinomiales, que reciben el nombre de ecuaciones de segundo grado o ecuaciones cuadráticas. Una ecuación cuadrática con una variable es cualquier ecuación que se pueda escribir de la forma: 
, donde x es una variable, en tanto que a, b y c son constantes. Nos referiremos a esta forma como la forma general de la ecuación cuadrática.
Raíz Cuadrada
Un tipo más sencillo de ecuación cuadrática, por su solución, corresponde a la forma especial en que falta el término con la variable de primer grado; o sea cuando está en la siguiente forma: 
El método de solución aprovecha directamente la definición de raíz cuadrada. El proceso se ilustra en el siguiente ejemplo:
Ejemplo 1
Resuelve por medio de la raíz cuadrada 
SOLUCIÓN:
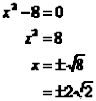
Ejemplo 2
Resuelve por medio de la raíz cuadrada 
SOLUCIÓN:
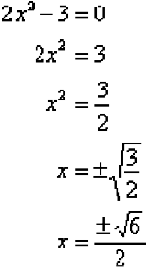
Ejemplo 3
Resuelve por medio de la raíz cuadrada 
SOLUCIÓN:
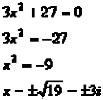
Factorización
Si los coeficientes a, b y c de la ecuación cuadrática 
son tales que la expresión 
puede escribirse como el producto de dos factores de primer grado con coeficientes enteros, dicha ecuación cuadrática podrá resolverse rápida y fácilmente. El método de resolución por factorización se basa en la siguiente propiedad de los números reales:
Si a y b son números reales, entonces:
a b = 0 si y solo si a = 0 o b = 0 (o ambos valen cero)
Esta propiedad se demuestra con facilidad: si a = 0, hemos concluido. Si a ≠ 0, multiplicamos ambos miembros de ab = 0 por 1/a, para obtener: b = 0.
Ejemplo 1
Resuelve por factorización 
SOLUCIÓN:
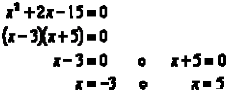
Ejemplo 2
Resuelve por factorización 
SOLUCIÓN:
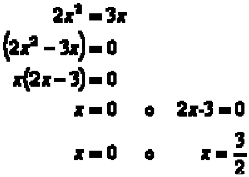
Ejemplo 3
Resuelve por factorización 
SOLUCIÓN: El polinomio no se puede factorizar con coeficientes enteros; por tanto, debe de usarse otro método para encontrar la solución.
Completando el trinomio cuadrado perfecto
El método de compleción del cuadrado se basa en el proceso de transformar la cuadrática general 
para que quede así: 
. Donde A y B son constantes. Esta última ecuación se puede resolver fácilmente por medio de la raíz cuadrada, como se explicó en la sección anterior. Así:
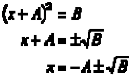
Antes de estudiar cómo se resuelve la primera parte, haremos una pausa breve para analizar un problema relacionado con el nuestro: ¿Qué número se le debe de sumar a 
para que el resultado sea el cuadrado de una expresión lineal? Hay una sencilla regla mecánica para encontrar tal número: se basa en los cuadrados de los siguientes binomios:
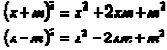
En ambos casos, observemos que, en el miembro derecho, el tercer término es el cuadrado de la mitad del coeficiente de x, que aparece en el segundo término. Esta observación nos lleva directamente a la regla:
Para completar el cuadrado de una expresión cuadrática de la forma 
Se suma el cuadrado de la mitad del coeficiente de x, o sea: 
o sea 
Ejemplo 1
Completa el cuadrado de 
SOLUCIÓN: Sumamos el cuadrado de la mitad del coeficiente de x, usamos la forma 
, por lo que obtenemos:
Ejemplo 2
Completa el cuadrado de 
SOLUCIÓN: Sumamos ; o sea , así:
La resolución de ecuaciones cuadráticas por el método de compleción del cuadrado se ilustra mejor con ejemplos
Ejemplo 3
Resuelve 
por el método de compleción del cuadrado
SOLUCIÓN:
Sumamos 2 a ambos miembros de la ecuación para eliminar -2 del miembro izquierdo.
Para completar el cuadrado del miembro izquierdo, sumamos el cuadrado del coeficiente de x, en ambos miembros de la ecuación.
Factorizamos el miembro izquierdo.
Resolvemos por medio de la raíz cuadrada.
Ejemplo 4
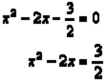
Resuelve 
por el método de compleción del cuadrado
SOLUCIÓN:
Observa que el coeficiente de x2 no es 1. En tal caso, dividimos todos los términos entre el
coeficiente principal y proseguimos como en el ejemplo anterior.
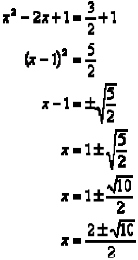
Formula cuadrática
Para obtener la fórmula para resolver ecuaciones de segundo grado, tomamos la ecuación general 
y resolvemos para x, en función de los coeficientes a, b y c, por el método de compleción del cuadrado; de esta manera obtenemos una fórmula que podremos memorizar y utilizar siempre que se conozca el valor de a, b y c.
Para empezar, haremos igual a 1 el coeficiente principal. Para ello, multiplicamos por 1/a ambos miembros de la ecuación. Queda así:
Sumamos –c/a a ambos miembros de la ecuación para suprimir c/a del miembro izquierdo.
Ahora completamos el cuadro del miembro izquierdo; para ello, sumamos a cada miembro del cuadrado de la mitad del coeficiente de x;
Luego factorizamos el miembro izquierdo de la ecuación y la resolvemos por medio de la raíz cuadrada.
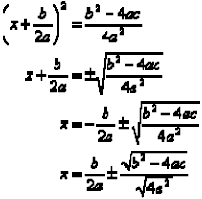
Obtenemos esto:
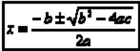
Esta última ecuación se llama fórmula cuadrática. Es necesario memorizarla y emplearla para resolver ecuaciones cuadráticas, cuando no dan resultado métodos más sencillos. Observa que b2-4ac recibe el nombre de discriminante y nos proporciona la siguiente información útil respecto de las raíces:
b2 - 4ac
ax2 + box + c = 0
Positivo
Dos soluciones reales Cero
Una solución real Negativo
Dos soluciones complejas
Ejemplo 1
Resuelve 
por la fórmula cuadrática
SOLUCIÓN: anotamos la fórmula cuadrática e identificamos a=2, b=-4 y c=-3.
Sustituimos la fórmula y simplificamos.
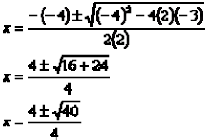
Ejemplo 2
Resuelve 
por la fórmula cuadrática
SOLUCIÓN: 
escribimos en la forma general e identificamos a = 1, b = -6 y c = 11
Sustituimos la fórmula y simplificamos.
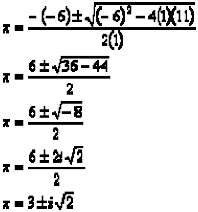
Link: https://www.matesfacil.com/resueltos-ecuaciones-segundo-grado.htm
Link: http://www.vadenumeros.es/tercero/ecuaciones-de-segundo-grado.htm
Relaciones de proporcionalidad directa
Para comprender el concepto de proporcionalidad, directa o inversa, debemos comenzar por comprender el concepto de razón.
Razón y proporción numérica
Razón entre dos números
Siempre que hablemos de Razón entre dos números nos estaremos refiriendo al cociente (el resultado de dividirlos) entre ellos.
Entonces:
Razón entre dos números a y b es el cociente entre 
Por ejemplo, la razón entre 10 y 2 es 5 , ya que 
Y la razón entre los números 0,15 y 0,3 es 
Proporción numérica
Ahora, cuando se nos presentan dos razones para ser comparadas entre sí, para ver cómo se comportan entre ellas, estaremos hablando de una proporción numérica.
Entonces:
Los números a, b, c y d forman una proporción si la razón entre a y b es la misma que entre c y d.
Es decir 
Se lee “ a es a b como c es a d”
Los números 2, 5 y 8, 20 forman una proporción, ya que la razón entre 2 y 5 es la misma que la razón entre 8 y 20.
Es decir 
En la proporción Hay cuatro términos; a y d se llaman extremos, c y b se llaman medios.
La propiedad fundamental de las proporciones es: en toda proporción, el producto de los extremos es igual al de los medios.
Así, en la proporción anterior 
Se cumple que el producto de los extremos nos da 2 x 20 = 40 y el producto de los medios nos da 5 x 8 = 40
Comprendido el concepto de proporción como una relación entre números o magnitudes, ahora veremos que esa relación puede darse en dos sentidos:
Las dos magnitudes pueden subir o bajar (aumentar o disminuir) o bien si una de las magnitudes sube la otra bajo y viceversa.
Si ocurre, como en el primer caso, que las dos magnitudes que se comparan o relacionan pueden subir o bajar en igual cantidad, hablaremos de Magnitudes directamente proporcionales.
Si ocurre como en el segundo caso, en que si una magnitud sube la otra baja en la misma cantidad, hablaremos de Magnitudes inversamente proporcionales.
MAGNITUDES DIRECTAMENTE PROPORCIONALES
Si dos magnitudes son tales que a doble, triple... cantidad de la primera corresponde doble,
triple... cantidad de la segunda, entonces se dice que esas magnitudes son directamente proporcionales.
Ejemplo
Un saco de papas pesa 20 kg. ¿Cuánto pesan 2 sacos?
Un cargamento de papas pesa 520 kg ¿Cuántos sacos de 20 kg se podrán hacer?
Número de sacos | 1 | 2 | 3 | ... | 26 | ... |
Peso en kg | 20 | 40 | 60 | ... | 520 | ... |
Para pasar de la 1ª fila a la 2ª basta multiplicar por 20 Para pasar de la 2ª fila a la 1ª dividimos por 20
Observa que 
Las magnitudes número de sacos y peso en kg son directamente proporcionales.
La constante de proporcionalidad para pasar de número de sacos a kg es 20.
Esta manera de funcionar de las proporciones nos permite adentrarnos en lo que llamaremos Regla de tres y que nos servirá para resolver una gran cantidad de problemas matemáticos.
REGLA DE TRES SIMPLE DIRECTA
Ejemplo 1
En 50 litros de agua de mar hay 1.300 gramos de sal. ¿Cuántos litros de agua de mar contendrán 5.200 gramos de sal?
Como en doble cantidad de agua de mar habrá doble cantidad de sal; en triple, triple, etc. Las magnitudes cantidad de agua y cantidad de sal son directamente proporcionales.
Si representamos por x el número de litros que contendrá 5200 gramos de sal, y formamos la siguiente tabla:
Litros de agua | 50 | x |
Gramos de sal | 1.300 | 5.200 |
Se verifica la proporción: 
Y como en toda proporción el producto de medios es igual al producto de extremos (en palabras simples, se multiplican los números en forma cruzada) resulta:
50 por 5.200 = 1.300 por x
Es decir 
En la práctica esto se suele disponer del siguiente modo:
Esta forma de plantear y resolver problemas sobre proporciones se conoce con el nombre de regla de tres simple directa.
Ejemplo 2
Un automóvil gasta 5 litros de bencina cada 100 km. Si quedan en el depósito 6 litros, ¿cuántos kilómetros podrá recorrer el automóvil?
Luego, con 6 litros el automóvil recorrerá 120 km
MAGNITUDES INVERSAMENTE PROPORCIONALES
Si dos magnitudes son tales que a doble, triple... cantidad de la primera corresponde la mitad, la tercera parte... de la segunda, entonces se dice que esas magnitudes son inversamente proporcionales.
Ejemplo
Si 3 hombres necesitan 24 días para hacer un trabajo, ¿cuántos días emplearán 18 hombres para realizar el mismo trabajo?
En este caso a doble número de trabajadores, el trabajo durará la mitad; a triple número de trabajadores, el trabajo durará la tercera parte, etc. Por tanto, las magnitudes son inversamente proporcionales (también se dice que son indirectamente proporcionales).
Formamos la tabla:
Hombres | 3 | 6 | 9 | ... | 18 |
Días | 24 | 12 | 8 | ... | ? |
Vemos que los productos 3 por 24 = 6 por 12 = 9 por 8 = 72 Por tanto 18 por x = 72
O sea que los 18 hombres tardarán 4 días en hacer el trabajo
Nótese que aquí la constante de proporcionalidad, que es 72, se obtiene multiplicando las magnitudes y que su producto será siempre igual.
Importante:
Como regla general, la constante de proporcionalidad entre dos magnitudes inversamente proporcionales se obtiene multiplicando las magnitudes entre sí, y el resultado se mantendrá constante.
Relaciones de proporcionalidad en el plano cartesiano
Una proporción es la igualdad de dos razones.
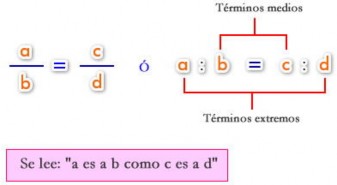
Propiedad fundamental
En toda proporción, el producto de los términos medios es igual al producto de los términos extremos (Teorema fundamental de las proporciones). Es decir:
Ejemplo: Si tenemos la proporción:
Y le aplicamos la propiedad fundamental señalada queda: 3 • 20 = 4 • 15, es decir, 60 = 60.
Esta es la propiedad que nos permite detectar si dos cantidades presentadas como proporción lo son verdaderamente.
Proporcionalidad directa
Dos variables (una independiente x y la otra dependiente y) son directamente proporcionales si el cociente (división) entre los valores respectivos de cada una de las variables es constante.
Y / x = k
Además, al aumentar o disminuir una de ellas, la otra aumenta o disminuye, respectivamente, en la misma razón.
Ejemplo:
- Indica si las variables son directamente proporcionales
La medida del lado de un cuadrado y su perímetro:
Respuesta Sí, porque a mayor longitud de sus lados mayor perímetro. (Si una variable aumenta la otra aumenta en la misma razón).
El número de trabajadores y los días que se demoran en hacer un trabajo, si todos trabajan de igual manera: Respuesta: No, porque a mayor cantidad de trabajadores menos cantidad de días. (Si una variable aumenta, la otra disminuye en la misma razón).
En el caso de las funciones esta proporcionalidad directa se puede representar como una función de la forma
y = k x
Dónde:
y: variable dependiente.
X: variable independiente.
K: constante de proporcionalidad.
Por ejemplo: si tenemos la siguiente función:
y = 3 x
La constante de proporcionalidad sería 3.
¿Cómo se calcula la constante de proporcionalidad?
Como y = k x entonces: k = y / x
Calcula la constante de proporcionalidad:
x 3 6 7
y 6 12 14
k = 6 / 3
k = 2
El cociente de las dos magnitudes es siempre el mismo (constante)
Gráfico de proporcionalidad directa
El gráfico correspondiente a una relación de proporcionalidad directa es una línea recta que pasa por el punto de origen de un sistema de coordenadas cartesianas.
En una función de prorcionalidad directa, si una de las variables aumenta, la otra también aumenta en un mismo factor; y si una de las variables disminuye, la otra disminuye en un mismo factor.
Ejemplo:
Juan ha utilizado 20 huevos para hacer 4 tortillas iguales. ¿Cuántos huevos necesita para hacer 6 tortillas? ¿Y para hacer 2?
Grafica los resultados hasta 6 tortillas.
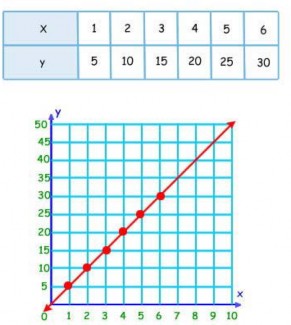
Como puedes ver, el gráfico es una línea recta que pasa por el origen. Además si nos fijamos en la tabla, nos podemos dar cuenta que el cociente (división) entre las dos magnitudes (y / x) es constante. En este caso el valor de la constante de proporcionalidad es 5.
Proporcionalidad inversa
Dos variables (una independiente x y la otra dependiente y) son inversamente proporcionales si el producto entre los valores respectivos de cada una de las variables es constante.
(x • y = k)
Además, en una función de proporcionalidad inversa, si una de las variables aumenta, la otra disminuye en un mismo factor; y si una de las variables disminuye, la otra aumenta en un mismo factor.
Esta relación de proporcionalidad inversa se puede representar como una función de la forma:
y = k / x
Donde:
y : variable dependiente. x: variable independiente.
k : constante de proporcionalidad.
Ejemplos:
Indica si las variables son inversamente proporcionales.
El número de albañiles y el tiempo empleado en hacer el mismo edificio.
Respuesta: Son inversamente proporcionales, ya que, con el doble, triple... número de albañiles se tardará la mitad, tercera parte de tiempo en construir el mismo edificio.
La velocidad de un auto y el trayecto recorrido en el mismo tiempo.
Respuesta: No es inversa ya que, a tiempo constante, con el doble o el triple... de la velocidad, el auto recorrerá el doble, triple... de espacio.
La velocidad de un auto y el tiempo empleado en recorrer el mismo trayecto.
Respuesta: Son inversamente proporcionales, ya que, a espacio constante, con el doble, triple... velocidad, el auto tardará la mitad, tercera parte... de tiempo en recorrerlo.
2.2- Gráfico de proporcionalidad inversa
La representación gráfica de esta función son puntos que pertenecen a una curva, llamada hipérbola.
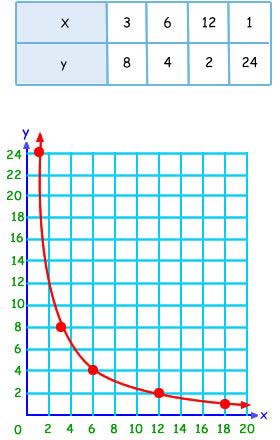
Resumen: Observa el siguiente cuadro comparativo:
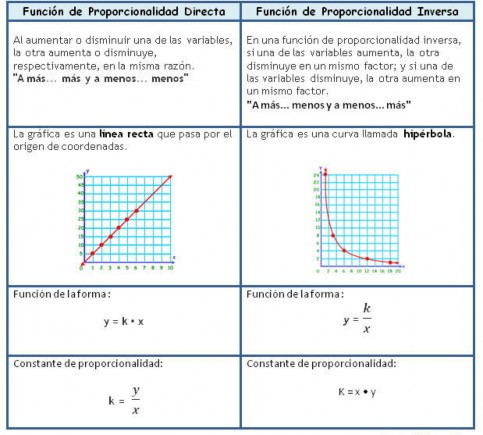
Preguntas:
Si 5 m de género valen $8500, ¿cuánto valen 8 m? R: valen $13600
Veinte alumnos hicieron una excursión y consumieron 15 botellas de jugo. ¿Cuántas botellas de jugo se habrían consumido, si hubieran ido los 50 alumnos del curso? R: 38 botellas
A cierta hora de un día asoleado, una persona, de 1,75 m de altura, proyecta una sombra de 1,25 m de longitud. Calcula la altura de un árbol del lugar que, en el mismo momento, tiene una sombra de 12 m de largo. R: 16,8 metros
Una piscina con un largo de 12cm y un ancho de 4cm., dibujada en un plano. Si en la realidad el largo es 36m, ¿cuál es el ancho? R: 12 metros
Rosa pesa 48 kilos y José pesa 52 kilos. Dividir una barra de chocolate de 200 gramos en la misma razón que sus pesos. R: 96 y 104 gramos
Con el dinero que tengo, puedo comprar 20 chocolates a $ 20 cada uno. Si los chocolates suben a $ 25,
¿cuántos podré comprar? R: puede comprar 16 chocolates
Si 25 telares producen cierta cantidad de tela en 60 horas, ¿cuántas horas emplearán 42 telares iguales en producir la misma cantidad de tela? R: 35 horas, 42 minutos y 52 segundos
Dos ruedas dentadas están engranadas. La primera tiene 12 dientes y la segunda 28. ¿Cuántas vueltas habrá dado la segunda, cuando la primera ha dado 84 vueltas? R: 36 vueltas
Link: https://www.portaleducativo.net/octavo-basico/806/Relacion-de-proporcionalidad-directa-e-inversa
Manejo de la Información Estadística
Análisis de la Información estadística: Índices
La investigación cuya finalidad es: el análisis o experimentación de situaciones para el descubrimiento de nuevos hechos, la revisión o establecimiento de teorías y las aplicaciones prácticas de las mismas, se basa en los principios de Observación y Razonamiento y necesita en su carácter científico el análisis técnico de Datos para obtener de ellos información confiable y oportuna.
Este análisis de Datos requiere de la Estadística como una de sus principales herramientas, por lo que los investigadores de profesión y las personas que de una y otra forma la realizan requieren además de los conocimientos especializados en su campo de actividades, del manejo eficiente de los conceptos, técnicas y procedimientos estadísticos.
MUESTREO
El muestreo es por lo tanto una herramienta de la investigación científica, cuya función básica es determinar que parte de una población debe examinarse, con la finalidad de hacer inferencias sobre dicha población. La muestra debe lograr una representación adecuada de la población, en la que se reproduzca de la mejor manera los rasgos esenciales de dicha población que son importantes para la investigación. Para que una muestra sea representativa, y por lo tanto útil, debe de reflejar las similitudes y diferencias encontradas en la población, es decir ejemplificar las características de ésta.
En estadística se conoce como muestreo a la técnica para la selección de una muestra a partir de una población. Al elegir una muestra aleatoria se espera conseguir que sus propiedades sean extrapola bles a la población. Este proceso permite ahorrar recursos, y a la vez obtener resultados parecidos a los que se alcanzarían si se realizase un estudio de toda la población. Cabe mencionar que para que el muestreo sea válido y se pueda realizar un estudio adecuado (que consienta no solo hacer estimaciones de la población sino estimar también los márgenes de error correspondientes a dichas estimaciones), debe cumplir ciertos requisitos. Nunca podremos estar enteramente seguros de que el resultado sea una muestra representativa, pero sí podemos actuar de manera que esta condición se alcance con una probabilidad alta. En el muestreo, si el tamaño de la muestra es más pequeño que el tamaño de la población, se puede extraer dos o más muestras de la misma población. Al conjunto de muestras que se pueden obtener de la población se denomina espacio muestral. La variable que asocia a cada muestra su probabilidad de extracción, sigue la llamada distribución maestral.
EJEMPLOS:
1.-Suponga que estamos investigando sobre el porcentaje de alumnos que trabajan de una población de 20 alumnos de una Universidad
Base de datos de la población:
Nombre Alumno ¿Trabaja?
Juan SI
María NO
Alicia NO
Fernanda NO
Pedro NO
Julio SI
Marcos NO
Rosa NO
Alberto SI
Fabián NO
Jorge SI
Ana NO
José NO
Laura NO
Carlos NO
Enrique NO
Miguel NO
Carmen SI
Victoria SI
Marcelo SI
2.-Se tiene a la siguiente población de personas clasificadas como consumidores de drogas:
Nombre Droga
Felipe Alcohol
Wilma Marihuana
José Pasta Base
Viviana Cocaína
Pablo Alcohol
Rodrigo Marihuana
Carlos Éxtasis
Catherine Alcohol
Claudia Marihuana
Valentina Neoprén
Enrique Marihuana
3.-
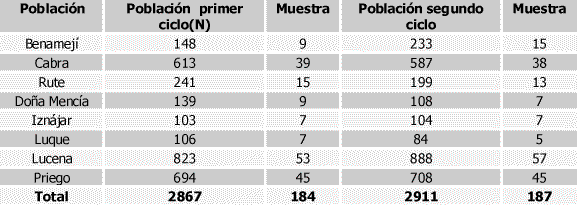
FRECUENCIA
En Estadística, frecuencia es el número de veces que el valor de una variable se repite. Se distinguen dos tipos principales de frecuencia: relativa y absoluta.
Frecuencia de clase
Es el número de mediciones que se pueden agrupar en una clase en una tabla o distribución de frecuencia Clase
Es un intervalo o subconjunto de una escala que se utiliza para comparar mediciones o características que pertenecen a un elemento muestral y determinar cuáles por su magnitud o cualidad le pertenece
Frecuencia relativa
Es el resultado de la división entre el valor de la frecuencia absoluta (ni) y el tamaño de la muestra (N). Se suele representar de esta forma: fi. Puede aparecer de forma decimal, como fracción o como un porcentaje.
Frecuencia relativa acumulada
Es la suma de la frecuencia relativa de todas las clases anteriores a la clase más la de esta
Formula:
Frecuencia Relativa 
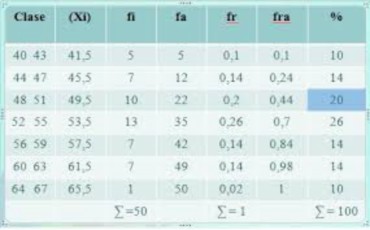
3.-
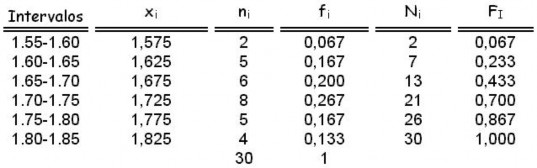
DISTRIBUCIÓN DE FRECUENCIA
Una distribución de frecuencias o tabla de frecuencias es una ordenación en forma de tabla de los datos estadísticos, asignando a cada dato su frecuencia correspondiente. Frecuencia absoluta La frecuencia absoluta es el número de veces que aparece un determinado valor en un estudio estadístico. Se representa por fi.La suma de las frecuencias absolutas es igual al número total de datos, que se representa por N.Para indicar resumidamente estas sumas se utiliza la letra griega Σ (sigma mayúscula) que se
lee suma o sumatoria.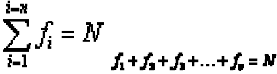 
Ejemplos:
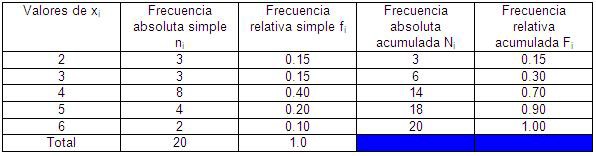
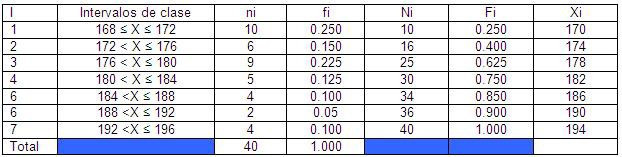
REPRESENTACIÓN GRÁFICA E INTERPRETACIÓN
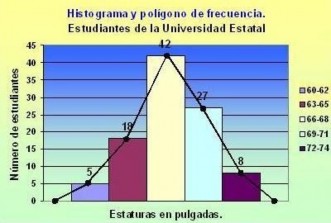
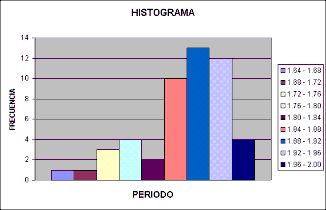
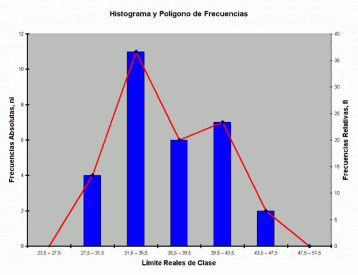
Histograma de Frecuencias
Los histogramas son diagramas de barras verticales en los que se construyen barras rectangulares en los límites de cada clase. La variable aleatoria o fenómeno de interés se despliega a lo largo del eje horizontal; el eje vertical representa el número, proporción o porcentaje de observaciones por intervalo de clase, dependiendo de si el histograma particular, es un histograma de frecuencia, un histograma de frecuencia relativa o histograma de porcentaje.
Representaciones tabulares, frecuencias Una vez obtenida una muestra de cualquier población y observados los valores que toma la variable en los individuos de la muestra, estos valores se suelen ordenar. Si la variable es cuantitativa la ordenación será de menor a mayor.
Frecuencia absoluta ni.- es el número de veces que aparece en la muestra dicho valor de la variable. Frecuencias acumuladas fi.- la suma de cada frecuencia con la frecuencia de la clase contigua superior.
Frecuencias relativas Ni.- Dividiendo cada frecuencia entre el número total de observaciones y multiplicándolas por l00 para tenerlas en forma de porcentaje.
Frecuencias relativas acumuladas Fi.- La suma de cada frecuencia relativa con la frecuencia relativa de la clase contigua superior. También se pueden obtener dividiendo cada frecuencia acumulada entre el total de frecuencias por l00.
La distribución de frecuencia es la representación estructurada, en forma de tabla, de toda la información que se ha recogido sobre la variable que se estudia en la muestra o población originales.
Ejemplos:
1.-
Gráficas de barra y circulares
DIAGRAMA DE BARRAS O DE COLUMNAS:
Es una forma de representar gráficamente un conjunto de datos o valores, está formado por barras rectangulares de longitudes proporcionales a los valores representados, los cuales pueden orientarse verticalmente u horizontalmente.
Los gráficos de barras son utilizados para comparar dos o más datos o valores.
EJEMPLO: en una empresa se desea conocer el color de los ojos de sus empleados, se observan 50 empleados y se obtiene el siguiente resultado.
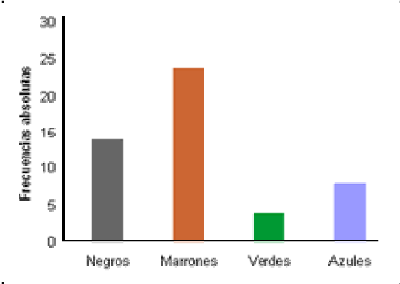
Empleados
Color
ojos
Negros 14
Marrones 24
Verdes 4
Azules 8
DIAGRAMA LINEAL O GRÁFICO DE LÍNEAL:
Se compone de una serie de datos representados por puntos, unidos por segmentos lineales. Mediante este gráfico se puede comprobar rápidamente el cambio de tendencia de los datos. El diagrama lineal se suele utilizar con variables cuantitativas, para ver su comportamiento en el transcurso del tiempo. Por ejemplo, en las series temporales mensuales, anuales, trimestrales, etc.
EJEMPLO:
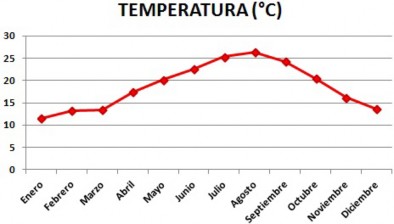
DIAGRAMA CIRCULAR (también llamado diagrama de sectores o diagrama de pastel):
Sirve para representar variables cualitativas o discretas. Se utiliza para representar la proporción de elementos de cada uno de los valores de la variable. Consiste en partir el círculo en porciones proporcionales
a la frecuencia relativa. Entiéndase como porción la parte del círculo que representa a cada valor que toma la variable.
Cálculo de los sectores:
Un círculo completo son 360º (o 2π radianes). El ángulo de cada porción debe ser proporcional a la frecuencia de cada valor. Por ejemplo, si un valor representa un 50% del total de elementos, su sector del círculo tendrá un ángulo de 180º (o π radianes).
Sea (X1, X2,…, XN) un conjunto de elementos. La fórmula para calcular el ángulo de cada sector es la siguiente:
El ángulo de cada sector se calcula como 360º dividido por el total de sujetos (N) y multiplicado por la frecuencia absoluta (ni), o bien el producto de la frecuencia relativa (fi) por 360º. También podemos calcular el ángulo en radianes:
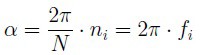
EJEMPLO:
Los continentes suponen el 29,1% de superficie de la Tierra, el resto es agua. Supongamos que se pretende representar mediante un diagrama circular la proporción de superficie de cada continente respecto a la superficie de todos los continentes.
Para dibujar el diagrama, calcula el ángulo de cada uno de los sectores (que serán Europa, África, América, Asia, Oceanía, la Antártida). Se obtiene la siguiente tabla:
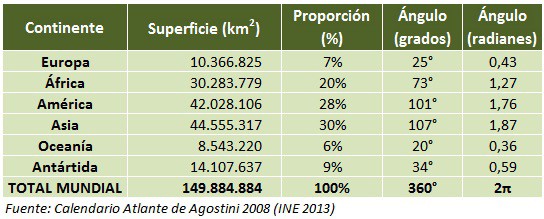
Una vez calculados los ángulos, puede representarlos gráficamente. El diagrama circular será el siguiente:
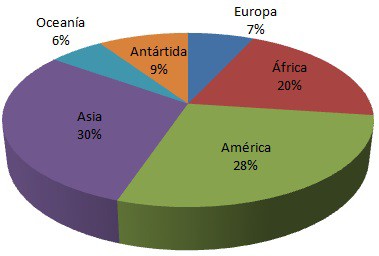
Link: https://sites.google.com/site/licelianarojano/3-unidad-estadistica/3-2-diagramas-de-barras-lineal- y-circular
Tablas de frecuencia absoluta y relativa
Las notas de un examen de matemáticas de 30 alumnos de una clase son las siguientes: 5, 3, 4, 1, 2, 8, 9, 8, 7, 6, 6, 7, 9, 8, 7, 7, 1, 0, 1, 5, 9, 9, 8, 0, 8, 8, 8, 9, 5, 7.
Ordenar los datos y calcular las frecuencias absolutas de cada nota.
Hacer un diagrama de barras de las frecuencias absolutas y dibujar el polígono de frecuencias.
Tabla para calcular la frecuencia relativa hi y las frecuencias acumuladas.
Ordenamos los datos contando los alumnos que han sacado un 0 han sido 2, un 1 han sido 3 y así sucesivamente. Construimos la tabla correspondiente: N: número total de datos N = 30.
xi: variable estadística, nota del examen.
fi: frecuencia absoluta, número de veces que se repite una nota. El sumatorio nos da los datos totales N = 30
Fi: frecuencia absoluta acumulada. Para calcularla vamos sumando los valores de la frecuencia absoluta fi.
F 2 = f 1 + f2 → 2 + 3 = 5; F 3 = F 2 + f 3 → 5 + 1 = 6
hi: frecuencia relativa. Cociente f i / N
Hi: frecuencia relativa acumulada
∑: sumatorio (suma de todos los datos de la columna correspondiente)
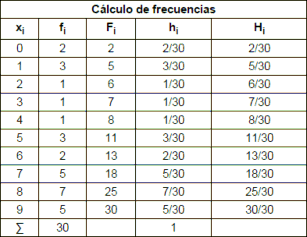
Diagrama de barras de frecuencia absoluta y polígona de frecuencias Representar el diagrama de barras de frecuencia absoluta
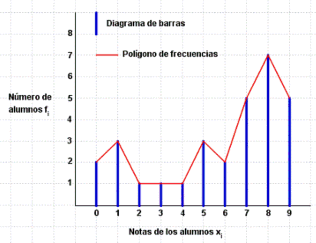
Dibujar el polígono de frecuencias
Variable cuantitativa continua
Se ha controlado el peso de 50 recién nacidos, obteniéndose los siguientes resultados:
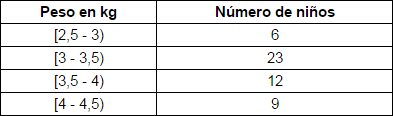
Formar la tabla de frecuencias.
Representar gráficamente la distribución.
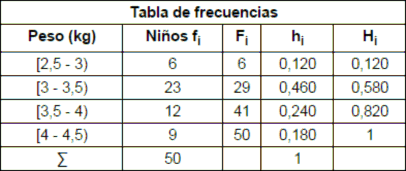
Tabla de frecuencias
La tabla de frecuencias se hace igual que en el ejemplo anterior
Histograma, gráfica de la distribución
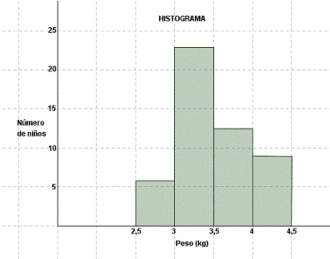
Interpretación
La mayoría de los niños, 23 tiene un peso comprendido entre 3 y 3,5 kg. Los niños con menor peso [2,5 - 3) son muy pocos solo 6.
Ejemplo de un diagrama de sectores
En un hipermercado se han producido las siguientes ventas en euros: juguetes 125, plantas 175, discos 250, alimentación 450.
Calcular las frecuencias, porcentajes y ángulo correspondiente.
Realizar un diagrama de sectores.
Colocamos los datos en una tabla.
Las variable xi son los productos vendidos.
Las frecuencias absolutas f i son las ventas en euros de cada producto.
Las frecuencias relativas hi se obtienen dividiendo las frecuencias absolutas entre el total de 1000
$.
El porcentaje % se calcula multiplicando la frecuencia relativa por 100. El ángulo se calcula multiplicando la frecuencia relativa por 360°.
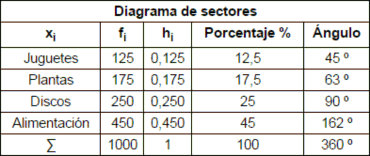
Diagrama de sectores
Para realizar el diagrama de sectores necesitamos conocer el ángulo. Para hallar el ángulo
multiplicamos la frecuencia relativa por 360 º que se corresponden con el total. Ver datos en la tabla.
Dibujamos los ángulos obtenidos en un círculo, unos a continuación de otros.
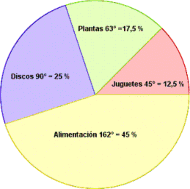
Link: http://www.vadenumeros.es/sociales/frecuencia-absoluta-relativa.htm
Medidas de tendencia central
Media, Mediana, Moda
Supóngase que un determinado alumno obtiene 35 puntos en una prueba de matemática. Este puntaje, por sí mismo tiene muy poco significado a menos que podamos conocer el total de puntos que obtiene una persona promedio al participar en esa prueba, saber cuál es la calificación menor y mayor que se obtiene, y cuán variadas son esas calificaciones.
En otras palabras, para que una calificación tenga significado hay que contar con elementos de referencia generalmente relacionados con ciertos criterios estadísticos.
Las medidas de tendencia central (media, mediana y moda) sirven como puntos de referencia para interpretar las calificaciones que se obtienen en una prueba.
Volviendo a nuestro ejemplo, digamos que la calificación promedio en la prueba que hizo el alumno fue de 20 puntos. Con este dato podemos decir que la calificación del alumno se ubica notablemente sobre el promedio. Pero si la calificación promedio fue de 65 puntos, entonces la conclusión sería muy diferente, debido a que se ubicaría muy por debajo del promedio de la clase.
En resumen, el propósito de las medidas de tendencia central es:
Mostrar en qué lugar se ubica la persona promedio o típica del grupo.
Sirve como un método para comparar o interpretar cualquier puntaje en relación con el puntaje central o típico.
Sirve como un método para comparar el puntaje obtenido por una misma persona en dos diferentes ocasiones.
Sirve como un método para comparar los resultados medios obtenidos por dos o más grupos.
Las medidas de tendencia central más comunes son:
La media aritmética: comúnmente conocida como media o promedio. Se representa por medio de una letra M o por una X con una línea en la parte superior.
La mediana: la cual es el puntaje que se ubica en el centro de una distribución. Se representa como Md.
La moda: que es el puntaje que se presenta con mayor frecuencia en una distribución. Se representa Mo.
De estas tres medidas de tendencia central, la media es reconocida como la mejor y más útil. Sin embargo, cuando en una distribución se presentan casos cuyos puntajes son muy bajos o muy altos respecto al resto
del grupo, es recomendable utilizar la mediana o la moda. (Porque dadas las características de la media, esta es afectada por los valores extremos).
La media es considerada como la mejor medida de tendencia central, por las siguientes razones: Los puntajes contribuyen de manera proporcional al hacer el cómputo de la media.
Es la medida de tendencia central más conocida y utilizada.
Las medias de dos o más distribuciones pueden ser fácilmente promediadas mientras que las medianas y las modas de las distribuciones no se promedian.
La media se utiliza en procesos y técnicas estadísticas más complejas mientras que la mediana y la moda en muy pocos casos.
Cómo calcular, la media, la moda y la mediana
Media aritmética o promedio
Es aquella medida que se obtiene al dividir la suma de todos los valores de una variable por la frecuencia total. En palabras más simples, corresponde a la suma de un conjunto de datos dividida por el número total de dichos datos.
Ejemplo 1:
En matemáticas, un alumno tiene las siguientes notas: 4, 7, 7, 2, 5, 3 n = 6 (número total de datos)
La media aritmética de las notas de esa asignatura es 4,8. Este número representa el promedio. Ejemplo 2:
Cuando se tienen muchos datos es más conveniente agruparlos en una tabla de frecuencias y luego calcular la media aritmética. El siguiente cuadro con las medidas de 63 varas de pino lo ilustra.
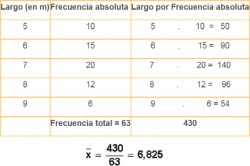
Se debe recordar que la frecuencia absoluta indica cuántas veces se repite cada valor, por lo tanto, la tabla es una manera más corta de anotar los datos (si la frecuencia absoluta es 10, significa que el valor a que corresponde se repite 10 veces).
Moda (Mo)
Es la medida que indica cual dato tiene la mayor frecuencia en un conjunto de datos; o sea, cual se repite más.
Ejemplo 1:
Determinar la moda en el siguiente conjunto de datos que corresponden a las edades de niñas de un Jardín Infantil.
5, 7, 3, 3, 7, 8, 3 , 5, 9, 5, 3, 4, 3
La edad que más se repite es 3, por lo tanto, la Moda es 3 (Mo = 3) Ejemplo 2:
20, 12, 14, 23, 78, 56, 96
En este conjunto de datos no existe ningún valor que se repita, por lo tanto, este conjunto de valores no tiene moda.
Mediana (Med)
Para reconocer la mediana, es necesario tener ordenados los valores sea de mayor a menor o lo contrario. Usted divide el total de casos (N) entre dos, y el valor resultante corresponde al número del caso que representa la mediana de la distribución.
Es el valor central de un conjunto de valores ordenados en forma creciente o decreciente. Dicho en otras palabras, la Mediana corresponde al valor que deja igual número de valores antes y después de él en un conjunto de datos agrupados.
Según el número de valores que se tengan se pueden presentar dos casos:
Si el número de valores es impar, la Mediana corresponderá al valor central de dicho conjunto de datos.
Si el número de valores es par, la Mediana corresponderá al promedio de los dos valores centrales (los valores centrales se suman y se dividen por 2).
Ejemplo 1:
Se tienen los siguientes datos: 5, 4, 8, 10, 9, 1, 2
Al ordenarlos en forma creciente, es decir de menor a mayor, se tiene: 1, 2, 4, 5 , 8, 9, 10 El 5 corresponde a la Med, porque es el valor central en este conjunto de datos impares. Ejemplo 2:
El siguiente conjunto de datos está ordenado en forma decreciente, de mayor a menor, y corresponde a un conjunto de valores pares, por lo tanto, la Med será el promedio de los valores centrales.
21, 19, 18, 15, 13, 11, 10, 9, 5, 3
Ejemplo 3:
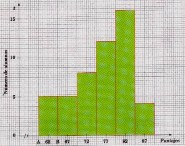
Interpretando el gráfico de barras podemos deducir que:
5 alumnos obtienen puntaje de 62
5 alumnos obtienen puntaje de 67
8 alumnos obtienen puntaje de 72
12 alumnos obtienen puntaje de 77
16 alumnos obtienen puntaje de 82
4 alumnos obtienen puntaje de 87 Lo que hace un total de 50 alumnos
Sabemos que la mediana se obtiene haciendo
Lo cual significa que la mediana se ubica en la posición intermedia entre los alumnos 25 y 26 (cuyo promedio es 25,5), lo cual vemos en el siguiente cuadro:
puntaje | alumnos |
62 | 1 |
62 | 2 |
62 | 3 |
62 | 4 |
62 | 5 |
67 | 6 |
67 | 7 |
67 | 8 |
67 | 9 |
67 | 10 |
72 | 11 |
72 | 12 |
72 | 13 |
72 | 14 |
72 | 15 |
72 | 16 |
72 | 17 |
72 | 18 |
77 | 19 |
77 | 20 |
77 | 21 |
77 | 22 |
77 | 23 |
77 | 24 |
77 | 25 |
77 | 26 |
77 | 27 |
77 | 28 |
77 | 29 |
77 | 30 |
82 | 31 |
82 | 32 |
82 | 33 |
82 | 34 |
82 | 35 |
82 | 36 |
82 | 37 |
82 | 38 |
82 | 39 |
82 | 40 |
82 | 41 |
82 | 42 |
82 | 43 |
82 | 44 |
82 | 45 |
82 | 46 |
87 | 47 |
87 | 48 |
87 | 49 |
87 | 50 |
El alumno 25 obtuvo puntaje de 77 El alumno 26 obtuvo puntaje de 77
Entonces, como el total de alumnos es par debemos promediar esos puntajes:
La mediana es 77, lo cual significa que 25 alumnos obtuvieron puntaje desde 77 hacia abajo (alumnos 25 hasta el 1 en el cuadro) y 25 alumnos obtuvieron puntaje de 77 hacia arriba (alumnos 26 hasta el 50 en el cuadro).
Nociones de probabilidad y muestreo
Muestra:
La muestra es una parte de la población, que es representativa de la misma. Entonces una muestra es una parte o un subconjunto de una población seleccionado con la finalidad de analizar y obtener propiedades de esta.
Muestreo: es el procedimiento mediante el cual se obtiene una muestra
Algunas razones que justifican el uso del muestreo son:
naturaleza destructiva del proceso de investigación
imposibilidad de revisar todos los elementos de la población.
Costo: al obtener los datos de una pequeña porción del total.
tiempo: al considerar solo una parte del total, su recolección y resumen se hará con mayor rapidez.
precisión: las posibilidades de usar personal más capacitado y supervisar cuidadosamente el trabajo de campo y el procesamiento de la información
Seleccionar una muestra adecuada:
Para seleccionar una muestra se deben tomar en cuenta algunas consideraciones elegir el tamaño de la muestra, lo cual depende no solo de la cantidad de información que se quiere conseguir, y el grado de certeza deseada, sino también del costo del muestreo y la selección de los elementos que la constituyen. Cualquiera sea el método elegido, el requisito más importante es que la muestra obtenida proporciona una imagen tan real como sea posible de aquella población que se ha sometido al muestreo.
Ya visto esto, este es otra definición del Muestreo:
Proceso de medición de la información en solo una parte de la población estadística. Se define como el proceso de seleccionar un número de observaciones de un grupo
Tipos de muestreo
Existen dos métodos para seleccionar muestra de poblaciones Muestreo no aleatorio:
Es práctica común seleccionar una muestra en forma intencional. De acuerdo a opiniones o criterios personales, fundamentalmente con el objeto de obtener información sin mucho costo.
Ejemplo: si estamos estudiando el número de personas que practican fútbol en una determinada región del país, tenemos que buscar específicamente a una persona que practique fútbol, es decir el proceso de elegir a quien se le aplica la encuesta no es aleatorio, a diferencia de que se pregunte qué opina de la selección de fútbol de Venezuela, que la forma de elegir al encuestado si es aleatorio.
Para ser no aleatorio tiene que cumplir con estas características:
la muestra consiste en los elementos que estén más a la mano.
se seleccionan un grupo de unidades tipo.
La muestra está compuesta por voluntarios.
La muestra es restringidas a la parte de la población que es fácilmente accesible. 
Muestreo aleatorio:
En el cual todos los elementos de la población tienen la oportunidad de ser escogidos para la muestra. Este procedimiento da a cada elemento de la población una probabilidad de ser seleccionado. Dentro de este tipo se encuentran:
muestreo aleatorio simple:
Permite que cada muestra posible pueda ser elegida con la misma probabilidad. Por su parte cada elemento de la población tiene la misma oportunidad igual de ser incluido en la muestra.
muestreo sistemático:
En el cual los elementos que se muestrearan se seleccionan de la población en un intervalo uniforme que se mide con respecto al tiempo, al orden o al espacio.
Muestreo estratificado:
Método en el que la población se divide en grupos homogéneos, o estratos. Aquí la variabilidad dentro de cada grupo es pequeña y entre los grupos es grande.
Muestreo por conglomerado:
Método en el que la población se divide en grupos o racimos de elementos, y luego se selecciona una muestra aleatoria de estos racimos. Aquí la variabilidad dentro de cada grupo es grande y entre los grupos es pequeño.
Link: http://frecuenciaestadistica.blogspot.mx/
Link: https://www.youtube.com/watch?v=Soj-aMLwCgQ
Link: https://es.slideshare.net/produceideas/nociones-de-muestreo
Probabilidad
La probabilidad mide la frecuencia con la que ocurre un resultado en un experimento bajo condiciones suficientemente estables. La teoría de la probabilidad se usa extensamente en áreas como la estadística, la matemática, la ciencia y la filosofía para sacar conclusiones sobre la probabilidad de sucesos potenciales y la mecánica subyacente de sistemas complejos.
Interpretaciones
La palabra probabilidad no tiene una definición consistente. De hecho, hay dos amplias categorías de interpretaciones de la probabilidad: los frecuentistas hablan de probabilidades sólo cuando se trata de experimentos aleatorios bien definidos. La frecuencia relativa de ocurrencia del resultado de un experimento, cuando se repite el experimento, es una medida de la probabilidad de ese suceso aleatorio. Los bayesianos, no obstante, asignan las probabilidades a cualquier declaración, incluso cuando no implica un proceso aleatorio, como una manera de representar su verosimilitud subjetiva.
Historia
El estudio científico de la probabilidad es un desarrollo moderno. Los juegos de azar muestran que ha habido un interés en cuantificar las ideas de la probabilidad durante milenios, pero las descripciones matemáticas exactas de utilidad en estos problemas sólo surgieron mucho después.
Según Richard Jeffrey, “Antes de la mitad del siglo XVII, el término ‘probable’ (en latín probable) significaba aprobable, y se aplicaba en ese sentido, unívocamente, a la opinión y a la acción. Una acción u opinión probable era una que las personas sensatas emprenderían o mantendrían, en las circunstancias.”
Aparte de algunas consideraciones elementales hechas por Girolamo Cardano en el siglo XVI, la doctrina de las probabilidades data de la correspondencia de Pierre de Fermat y Blaise Pascal (1654). Christiaan Huygens (1657) le dio el tratamiento científico conocido más temprano al concepto. Ars Conjectandi (póstumo, 1713) de Jakob Bernoulli y Doctrine of Chances (1718) de Abraham de Moivre trataron el tema como una rama de las matemáticas. Véase El surgimiento de la probabilidad (The Emergence of Probability) de Ian Hacking para una historia de los inicios del desarrollo del propio concepto de probabilidad matemática.
La teoría de errores puede trazarse atrás en el tiempo hasta Opera Miscellanea (póstumo, 1722) de Roger Cotes, pero una memoria preparada por Thomas Simpson en 1755 (impresa en 1756) aplicó por primera vez la teoría para la discusión de errores de observación. La reimpresión (1757) de esta memoria expone los axiomas de que los errores positivos y negativos son igualmente probables, y que hay ciertos límites asignables dentro de los cuales se supone que caen todos los errores; se discuten los errores continuos y se da una curva de la probabilidad.
Pierre-Simon Laplace (1774) hizo el primer intento para deducir una regla para la combinación de observaciones a partir de los principios de la teoría de las probabilidades. Representó la ley de la probabilidad de error con una curva y = φ(x), siendo x cualquier error e y su probabilidad, y expuso tres propiedades de esta curva:
1. es simétrica al eje y; 2.el eje x es una asíntota, siendo la probabilidad del error \infty igual a 0; 3.la superficie cerrada es 1, haciendo cierta la existencia de un error.
Dedujo una fórmula para la media de tres observaciones. También obtuvo (1781) una fórmula para la ley de facilidad de error (un término debido a Lagrange, 1774), pero una que llevaba a ecuaciones inmanejables. Daniel Bernoulli (1778) introdujo el principio del máximo producto de las probabilidades de un sistema de errores concurrentes.
El método de mínimos cuadrados se debe a Adrien-Marie Legendre (1805), que lo introdujo en su Nouvelles méthodes pour la détermination des orbites des comètes (Nuevos métodos para la determinación de las órbitas de los cometas). Ignorando la contribución de Legendre, un escritor irlandés estadounidense, Robert Adrain, editor de “The Analyst” (1808), dedujo por primera vez la ley de facilidad de error,
Siendo c y h constantes que dependen de la precisión de la observación. Expuso dos demostraciones, siendo la segunda esencialmente la misma de John Herschel (1850). Gauss expuso la primera demostración que parece que se conoció en Europa (la tercera después de la de Adrain) en 1809. Demostraciones adicionales se expusieron por Laplace (1810, 1812), Gauss (1823), James Ivory (1825, 1826), Hagen (1837), Friedrich Bessel (1838), W. F. Donkin (1844, 1856) y Morgan Crofton (1870). Otros personajes que contribuyeron fueron Ellis (1844), De Morgan (1864), Glaisher (1872) y Giovanni Schiaparelli (1875). La fórmula de Peters (1856) para r, el error probable de una única observación, es bien conocida.
En el siglo XIX, los autores de la teoría general incluían a Laplace, Sylvestre Lacroix (1816), Littrow (1833), Adolphe Quetelet (1853), Richard Dedekind (1860), Helmert (1872), Hermann Laurent (1873), Liagre, Didion, y Karl Pearson. Augustus De Morgan y George Boole mejoraron la exposición de la teoría.
En la parte geométrica (véase geometría integral) los colaboradores de The Educational Times fueron influyentes (Miller, Crofton, McColl, Wolstenholme, Watson y Artemas Martin).
Teoría
La probabilidad constituye un importante parámetro en la determinación de las diversas causalidades obtenidas tras una serie de eventos esperados dentro de un rango estadístico.
Existen diversas formas como método abstracto, como la teoría Dempster-Shafer y la teoría de la relatividad numérica, esta última con un alto grado de aceptación si se toma en cuenta que disminuye considerablemente las posibilidades hasta un nivel mínimo ya que somete a todas las antiguas reglas a una simple ley de relatividad.
Formas Geométricas
Rectas y ángulos
Link: https://es.slideshare.net/mariaibarradiez/tema-5-rectas-y-angulos
Figuras planas Línea recta
La línea recta no tiene límites. Dos líneas rectas pueden ser:
Paralelas (nunca se cruzan)
Secantes (si se prolongan terminarían cruzándose):
Perpendiculares (se cortan formando 4 ángulos rectos)
Si la recta finaliza en un extremo se le llama semirrecta:
Un punto divide una recta en dos semirrectas.
Un trozo de recta limitada por los dos extremos se llama segmento.
La recta perpendicular al segmento que lo corta por la mitad se llama mediatriz.
Varios segmentos no alineados forman una línea poligonal, que puede ser:
Abierta
Cerrada
El punto en el que se unen dos segmentos se llama vértice.
Los ángulos pueden ser:
Agudo (menos de 90 grados)
Recto (90 grados)
Obtuso (más de 90 grados)
Llano (180 grados)
El ángulo viene limitado por un vértice y dos lados.
La recta que partiendo del vértice del ángulo lo divide en 2 partes iguales se llama bisectriz:
Link: http://www.aulafacil.com/cursos/l7763/primaria/matematicas-primaria/matematicas-quinto- primaria-10-anos/rectas-y-angulos
Un polígono está formado por una línea poligonal cerrada y la superficie interior. Todos sus lados tienen que ser líneas rectas.
Veamos ahora 2 figuras que no son polígonos:
Porque son líneas abiertas o porque alguno de sus lados no es una línea recta.
En un polígono se pueden distinguir:
Lados
Vértices
Ángulos
Diagonales (líneas rectas que unen dos vértices no consecutivos)
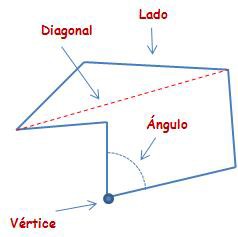
La suma de la longitud de sus lados se denomina perímetro.
La superficie interior de un polígono se llama área.
Según el número de lados, los polígonos se clasifican en:
Triángulo: 3 lados
Cuadrilátero: 4 lados
Pentágono: 5 lados
Hexágono: 6 lados
Heptágono: 7 lados
Octógono: 8 lados
Eneágono: 9 lados
Decágono: 10 lados
Hexágono regular
Pentágono regular
Cuadrilátero regular
Triángulo regular
Cuando todos los lados de un polígono son iguales se denomina polígono regular. También sus ángulos son iguales.
Heptágono regular Octógono regular
Como todos sus lados son iguales, su perímetro se puede calcular multiplicando la longitud de un lado por el número de lados:
Por ejemplo, el lado de este hexágono regular mide 5 cm, por lo que su perímetro será:
Perímetro = 5 x 6 (nº de lados) = 30 cm
1.- El triángulo
Los triángulos se pueden clasificar según sus lados:
Triángulo escaleno
Triángulo isósceles
Triángulo equilátero
Triángulo equilátero: todos sus lados son iguales Triángulo isósceles: tiene 2 lados iguales Triángulo escaleno: todos sus lados son diferentes
Los triángulos también se pueden clasificar según sus ángulos:
Triángulo rectángulo: un ángulo recto y dos agudos Triángulo acutángulo: todos sus ángulos son agudos Triángulo obtusángulo: uno de sus ángulos es obtuso
Triángulo obtusángulo
Triángulo acutángulo
Triángulo rectángulo
En el triángulo rectángulo podemos distinguir:
Los dos lados que forman el ángulo recto se denominan catetos
El lado opuesto al ángulo recto se denomina hipotenusa
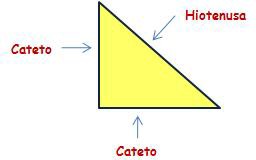
Se pueden clasificar en:
Paralelogramos: sus lados son paralelos dos a dos.
No paralelogramos: aquellos que no cumplen esta condición.
Los cuadriláteros paralelogramos se pueden clasificar en:
Cuadrado: 4 lados iguales y 4 ángulos rectos
Rectángulo: 4 lados iguales dos a dos y 4 ángulos rectos
Rombo: 4 lados iguales, y 2 ángulos agudos y 2 ángulos obtusos
Romboide: 4 lados iguales dos a dos, y 2 ángulos agudos y 2 ángulos obtusos
Romboide
Rombo
Rectángulo
Cuadrado
Los cuadriláteros no paralelogramos pueden ser:
Trapecio: Tiene 2 lados paralelos y los otros 2 no.
Trapezoide: Ninguno de sus lados es paralelo
Trapecio Trapezoide
El trapecio se puede clasificar en:
Trapecio rectángulo: 2 de sus ángulos son rectos
Trapecio isósceles: tiene 2 lados opuestos iguales y sus ángulos son iguales 2 a 2.
Trapecio escaleno: todos sus lados son diferentes
La circunferencia y el círculo
La circunferencia es una curva cerrada en la que todos sus puntos están a la misma distancia del centro. El interior de la circunferencia y la propia circunferencia forman un círculo.
Podemos distinguir los siguientes elementos:
Diámetro: Es la línea recta que va de lado a lado de la circunferencia pasando por el centro del círculo.
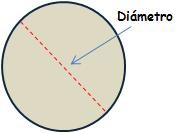
Radio: Es la línea recta que va desde el centro del círculo hasta la circunferencia.
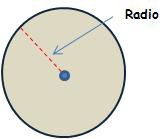
Cuerda: Es la línea recta que va de lado a lado de la circunferencia sin pasar por el centro del círculo.
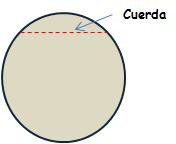
La mitad de un círculo se llama semicírculo:
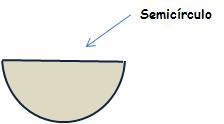
Una sección del círculo limitada por 2 radios y la circunferencia se llama sector circular.
Una sección del círculo limitada por una cuerda y la circunferencia se llama segmento circular.
Figura simétrica
Una figura simétrica es aquella en la que sus dos mitades son iguales. La línea que divide la figura en dos partes se denomina eje de simetría.
Figura simétrica
Figura no simétrica
Semejanza
Semejanza de Triángulos
Dos triángulos son semejantes si tienen dos ángulos iguales.
Dos triángulos son semejantes si tienen los lados proporcionales.
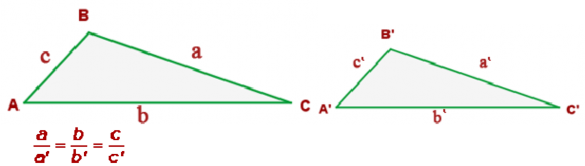
Dos triángulos son semejantes si tienen dos lados proporcionales y el ángulo comprendido entre ellos igual.
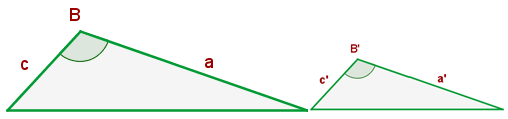
Ejercicios
Razona si son semejantes los siguientes triángulos:
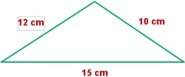
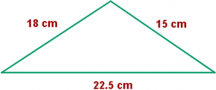
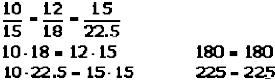
Son semejantes porque tienen los lados proporcionales.
180º − 100º − 60º = 20º
Son semejantes porque tienen dos ángulos iguales.
Son semejantes porque tienen dos lados proporcionales y un ángulo igual .
Link: http://www.vitutor.com/geo/eso/ss_2.html
Teorema de Pitágoras
Un triángulo rectángulo es un triángulo que tiene un ángulo recto, es decir de 90º.
En un triángulo rectángulo, el lado más grande recibe el nombre de hipotenusa y los otros dos lados se llaman catetos.
El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
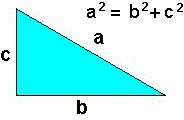
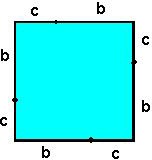
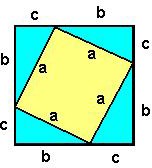
Si tenemos un triángulo rectángulo como el del dibujo del enunciado del teorema podemos construir un cuadrado que tenga de lado justo lo que mide el cateto b, más lo que mide el cateto c, es decir b+c, como en la figura de la derecha. El área de este cuadrado será (b+c)2.
Si ahora trazamos las hipotenusas de los triángulos rectángulos que salen tendremos la figura de la izquierda.
El área del cuadrado, que es la misma de antes, se puede poner ahora como la suma de las áreas de los cuatro triángulos rectángulos azules (base por altura partido por 2):
más el área del cuadrado amarillo . Es decir, el área del cuadrado grande también es el área del cuadrado pequeño más 4 veces el área del triángulo:
Podemos igualar las dos formas de calcular el área del cuadrado grande y tenemos:
Si ahora desarrollamos el binomio, nos queda:
Que después de simplificar resulta lo que estábamos buscando:
Link: https://www.um.es/docencia/pherrero/mathis/pitagoras/teorema.htm
Razones trigonométricas
Seno
El seno del ángulo B es la razón entre el cateto opuesto al ángulo y la hipotenusa .
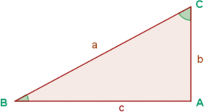
Se denota por sen B .
Coseno
El coseno del ángulo B es la razón entre el cateto contiguo al ángulo y la hipotenusa .
Se denota por cos B .
Tangente
La tangente del ángulo B es la razón entre el cateto opuesto al ángulo y el cateto contiguo al ángulo.
Se denota por tg B .
Cosecante
La cosecante del ángulo B es la razón inversa del seno de B .
Se denota por cosec B .
Secante
La secante del ángulo B es la razón inversa del coseno de B.
Se denota por sec B.
Cotangente
La cotangente del ángulo B es la razón inversa de la tangente de B.
Se denota por cotg B.
Razones trigonométricas en una circunferencia
Se llama circunferencia gonio métrica a aquélla que tiene su centro en el origen de coordenadas y su radio es la unidad .
En la circunferencia gonio métrica los ejes de coordenadas delimitan cuatro cuadrantes que se numeran en sentido contrario a las agujas del reloj.
QOP y TOS son triángulos semejantes.
QOP y T' OS′ son triángulos semejantes.
El seno es la ordenada.
El coseno es la abscisa.
-1 ≤ sen α ≤ 1
-1 ≤ cos α ≤ 1
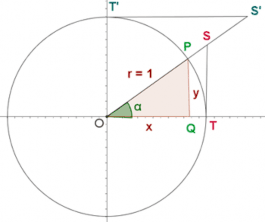
Signo de las razones trigonométricas
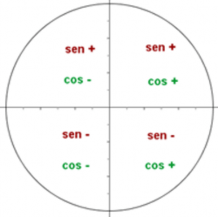
Tabla de razones trigonométricas
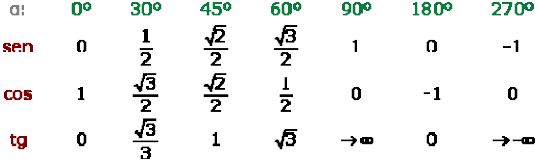
Relaciones entre las razones trigonométricas
cos² α + sen² α = 1
sec² α = 1 + tg² α
cosec² α = 1 + cotg² α
Relaciones entre las razones trigonométricas de algunos ángulos
Ángulos complementarios
Ángulos suplementarios
Ángulos que difieren en 180°
Ángulos opuestos
Ángulos negativos
Mayores de 360º
Ángulos que difieren en 90 º
Ángulos que suman en 270º
Ángulos que difieren en 270º
Razones trigonométricas de la suma y diferencia de ángulos
Razones trigonométricas del ángulo doble
Razones trigonométricas del ángulo mitad
Transformaciones de sumas en productos
Transformaciones de productos en sumas
Cuerpos geométricos
Calculo de perímetros
El perímetro de una figura geométrica plana es igual a la suma de las longitudes de sus lados .
Perímetro de un triangulo
Triángulo Equilátero | Triángulo Isósceles | Triángulo Escaleno |
|
|
|
|
|
|
Perímetro de un cuadrado
Perímetro de un rectángulo
Perímetro de un rombo
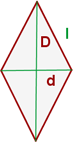
Perímetro del romboide
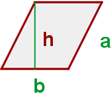
P = 2 · (a + b)
Perímetro de un pentágono regular
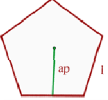
Perímetro de un hexágono regular
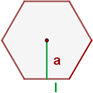
Perímetro de un polígono regular
n = número de lados
Longitud de una circunferencia
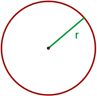
Cálculo de áreas
El área es la medida de la región o superficie encerrada por de una figura geométrica .
Áreas de las figuras planas
Área de un triángulo
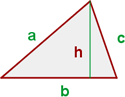
Área de un cuadrado
Área de un rectángulo
Área de un rombo
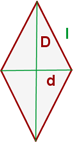
Área del romboide
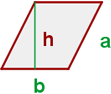
A = b · h
Área del trapecio
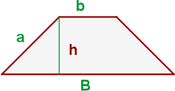
Área de un polígono regular
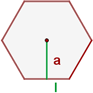
Área de un polígono
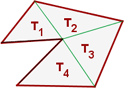
El área se
obtiene triangulando el
polígono y sumando el área de dichos triángulos.
A = T 1 + T 2 + T 3 + T 4
Área de un círculo
Área del sector circular
Área de un segmento circular
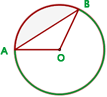
Áre a de l segmento circula r A B = Áre a de l secto r circula r AO B − Área de l triángul o AOB
Área de una corona circular
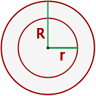
El área de una corona circular es
igual al área del círculo mayor menos el área del círculo menor .
Área de un trapecio circular
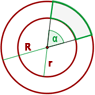
El área del trapecio circular es
igual al área del sector circular mayor menos el área del sector circular
menor .
Áreas de cuerpos geométricos
Área del Tetraedro
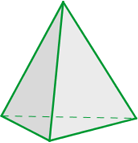
Área del cubo
Área del octaedro
Área del dodecaedro
Área del icosaedro
Área del prisma
Área del ortoedro
Área de la pirámide
Área del tronco de pirámide
Área del cilindro
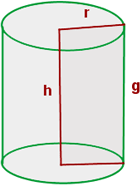
Área del cono
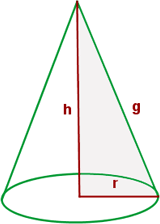
Área del tronco de cono
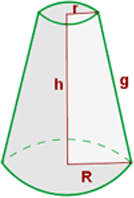
Área de la esfera
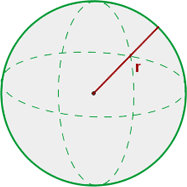
Área de la semiesfera
Área del huso esférico
Área del casquete esférico
Área de la zona esférica
Link: http://www.ditutor.com/geometria/areas.html
Cálculo de volúmenes
Link: https://www.youtube.com/watch?v=blWZiEUtB64
