

Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.
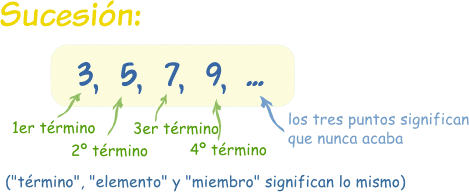
Si la sucesión sigue para siempre, es una sucesión infinita.
{1, 2, 3, 4 ,...} es una sucesión muy simple (y es una sucesión infinita)
{20, 25, 30, 35, ...} también es una sucesión infinita
{1, 3, 5, 7} es la sucesión de los 4 primeros números impares (y es una sucesión infinita)
{4, 3, 2, 1} va de 4 a 1 hacia atrás
{1, 2, 4, 8, 16, 32, ...} es una sucesión infinita donde vamos doblando cada término
{a, b, c, d, e} es la sucesión de las 5 primeras letras en orden alfabético
{a, l, f, r, e, d, o} es la sucesión de las letras en el nombre "alfredo"
{0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s (sí, siguen un orden, en este caso un orden alternativo)
Si no es una sucesión finita Ejemplos
Cuando decimos que los términos están "en orden", ¡nosotros somos los que decimos qué orden! Podría ser adelante, atrás... o alternando... ¡o el que quieras!
Una sucesión es muy parecida a un conjunto, pero con los términos en orden (y el mismo valor sí puede aparecer muchas veces).
Ejemplo: {0, 1, 0, 1, 0, 1, ...} es la sucesión que alterna 0s y 1s. El conjunto sería sólo {0,1}
Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.

Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:
Vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:
Probamos la regla: 2n
n | Término | Prueba |
1 | 3 | 2n = 2×1 = 2 |
2 | 5 | 2n = 2×2 = 4 |
3 | 7 | 2n = 2×3 = 6 |
Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:
Probamos la regla: 2n+1
n | Término | Regla |
1 | 3 | 2n+1 = 2×1 + 1 = 3 |
2 | 5 | 2n+1 = 2×2 + 1 = 5 |
3 | 7 | 2n+1 = 2×3 + 1 = 7 |
Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como
La regla para {3, 5, 7, 9, ...} es: 2n+1
Notación Posición del término

Es normal usar xn para los términos:
Así que para hablar del "quinto término" sólo tienes que escribir: x5
Entonces podemos escribir la regla para {3, 5, 7, 9, ...} en forma de ecuación, así:
xn = 2n+1 Ahora, si queremos calcular el 10º término, podemos escribir:
x10 = 2n+1 = 2×10+1 = 21
El ejemplo que acabamos de usar, {3,5,7,9,...}, es una sucesión aritmética (o progresión aritmética), porque la diferencia entre un término y el siguiente es una constante.
![]()
1, 4, 7, 10, 13, 16, 19, 22, 25, ...
Ejemplos
Esta sucesión tiene una diferencia de 3 entre cada dos términos. La regla es xn = 3n-2
![]()
3, 8, 13, 18, 23, 28, 33, 38, ...
Esta sucesión tiene una diferencia de 5 entre cada dos términos. La regla es xn = 5n-2
![]()
2, 4, 8, 16, 32, 64, 128, 256, ...
En una sucesión geométrica cada término se calcula multiplicando el anterior por un número fijo. Ejemplos:
![]()
La regla es xn = 2n
3, 9, 27, 81, 243, 729, 2187, ...
Esta sucesión tiene un factor 2 entre cada dos términos.
Esta sucesión tiene un factor 3 entre cada dos términos.
La regla es xn = 3n
![]()
4, 2, 1, 0.5, 0.25, ...
Esta sucesión tiene un factor 0.5 (un medio) entre cada dos términos.
La regla es xn = 4 × 2-n
![]()
1, 3, 6, 10, 15, 21, 28, 36, 45, ...
Esta sucesión se genera a partir de una pauta de puntos en un triángulo.
Añadiendo otra fila de puntos y contando el total encontramos el siguiente número de la sucesión.
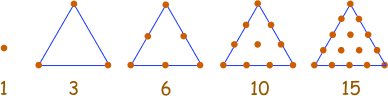
Pero es más fácil usar la regla
xn = n(n+1)/2
Ejemplo:
El quinto número triangular es x5 = 5(5+1)/2 = 15,
y el sexto es x6 = 6(6+1)/2 = 21 Números cuadrados
![]()
1, 4, 9, 16, 25, 36, 49, 64, 81, ...
El siguiente número se calcula elevando al cuadrado su posición.
La regla es xn = n2
![]()
1, 8, 27, 64, 125, 216, 343, 512, 729, ...
El siguiente número se calcula elevando al cubo su posición.
La regla es xn = n3
![]()
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...
El siguiente número se calcula sumando los dos que están antes de él. El 2 se calcula sumando los dos delante de él (1+1)
El 21 se calcula sumando los dos delante de él (8+13)
La regla es xn = xn-1 + xn-2
Esta regla es interesante porque depende de los valores de los términos anteriores. Por ejemplo el 6º término se calcularía así:
"Sucesiones" y "series" pueden parecer la misma cosa... pero en realidad una serie es la suma de una sucesión.
Sucesión: {1,2,3,4}
Serie: 1+2+3+4 = 10
Las series se suelen escribir con el símbolo Σ que significa "súmalos todos":
![]()
Esto significa "suma de 1 a 4" = 10
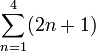
Esto significa "suma los cuatro primeros términos de la sucesión 2n+1"
Que son los cuatro primeros términos de nuestro ejemplo {3,5,7,9,...} = 3+5+7+9 = 24
Link: http://www.disfrutalasmatematicas.com/algebra/sucesiones-series.html Link: Video https://www.youtube.com/watch?v=Vlmgmlt7t9U
https://docs.google.com/document/d/1Cb2v41fx4cJOUVyV0i22OYwsIS7hxm_WrA2feboGBmA/edit?hl=es
Link: https://www.youtube.com/watch?v=22WHucXfMK0
El pensamiento espacial o razonamiento espacial, Es una habilidad que tenemos por lo menos la mayoría de las personas de visualizar algo inexistente, crearlo, poder manipularlo en el "espacio", típico.
Usualmente cuando alguien quiere explicar algún objeto mueve las manos para poder señalar dimensiones, forma, etc. Y si la otra persona receptora está en sintonía puede tener una visualización más acertada de lo que se le está explicando.
El pensamiento espacial constituye un componente esencial del pensamiento matemático, está referido a la percepción intuitiva o racional del entorno propio y de los objetos que hay en él. El desarrollo del pensamiento espacial, asociado a la interpretación y comprensión del mundo físico, permite desarrollar interés matemático y mejorar estructuras conceptuales y destrezas numéricas. El pensamiento espacial constituye un componente esencial del pensamiento matemático, está referido a la percepción intuitiva o racional del entorno propio y de los objetos que hay en él. El desarrollo del pensamiento espacial, asociado a la interpretación y comprensión del mundo físico, permite desarrollar interés matemático y mejorar estructuras conceptuales y destrezas numéricas.
El pensamiento espacial, se define como el conjunto de los procesos cognitivos mediante los cuales se construyen y se manipulan las representaciones mentales de los objetos del espacio, las relaciones entre ellos, sus transformaciones, y sus diversas traducciones o representaciones materiales en ella se contempla las actuaciones del sujeto en todas sus dimensiones y relaciones espaciales para interactuar de diversas maneras con los objetos situados en el espacio, desarrollar variadas representaciones y, a través de la coordinación entre ellas, hacer acercamientos conceptuales que favorezcan la creación y manipulación de nuevas representaciones mentales.
El pensamiento espacial pareciera haber sido tratado tradicionalmente como una habilidad carente de conocimiento o difícilmente asociable al mismo. En tal sentido, la tradición pedagógica ha perpetuado un error que de no haberse cometido podría significar que el estadio tecnológico actual fuese muy distinto.
Este pensamiento comprende el estudio geometría, los estudiantes aprenden acerca de las formas
Geométricas y sus estructuras y como analizar sus características y relaciones. La visualización espacial entendida como la construcción y la manipulación de representaciones mentales de objetos de dos y tres dimensiones y la percepción de los objetos desde diferentes perspectivas, es un aspecto muy importante de este pensamiento.
Hay que señalar que la representación visual, en su evolución, siempre intenta simular la perspectiva tridimensional. Y la capacidad para traducir entre representaciones bidimensionales y tridimensionales es fundamental para ampliar las posibilidades del pensamiento espacial. Por ejemplo: un mapa conceptual bien puede derivar en una red tridimensional, y un mapa mental bien podría ser un conjunto de terminales en el espacio alrededor de un núcleo.
En el pensamiento espacial se debe:
-Habilidad para imaginar una representación tridimensional desde distintas perspectivas
-Habilidad para visualizar - concreta mente e imaginariamente - efectos de reflexión e inversión de objetos- imágenes.
-Comprender objetos tridimensionales partiendo de gráficos bidimensionales y viceversa.
Se trata pues de ‘hacer cosas’, de moverse, dibujar, construir, producir y tomar de estos esquemas operatorios el material para la conceptualización o representación interna. Esta conceptualización va acompañada en un principio por gestos y palabras del lenguaje ordinario, hasta que los conceptos estén incipientemente construidos a un nivel suficientemente estable para que los alumnos mismos puedan proponer y evaluar posibles definiciones y simbolismos formales
Las relaciones son las distintas conexiones que podemos hacer entre los elementos.
Estas relaciones y elementos se agrupan en tres grandes bloques y que a la vez, según Piaget, determinan el orden en que son adquiridos por los niños:
Relaciones topológicas: Son aquellas relaciones que no varían por una deformación bicontinua (dos veces continua, que no varía ni por estirar ni por girar).
Ejemplos: Número de lados, abierto, cerrado, orden.
Relaciones proyectivas: Son las relaciones que varían al cambiar el punto de proyección (el punto de vista desde donde los miro).
Ejemplos: arriba, abajo, derecha, detrás, delante.
Relaciones métricas: Son todas las relaciones que dependen de medidas. Ejemplo: paralelo, ángulo recto.
Los ejercicios de razonamiento matemático miden la habilidad para procesar, analizar y utilizar información en la Aritmética, el Álgebra y la Geometría. Se ha demostrado que ambas habilidades se relacionan con el éxito en las materias que se estudian en el nivel universitario.
Habilidad Matemática es aquella en que el aspirante es capaz de comprender conceptos, proponer y efectuar algoritmos y desarrollar aplicaciones a través de la resolución de problemas. En estas se consideran tres aspectos.
Serie de términos formados de acuerdo con una ley.
Son figuras o trazos que siguen reglas o patrones determinados.
Hay que echar a andar nuestra imaginación al 100%, ya que se presentan trazos, recortes y dobleces sin tener que hacerlo físicamente.
En este tipo de problemas se debe aplicar conocimientos básicos de física, química y aritmética.
Link: Ejercicios: http://www.cem.itesm.mx/venalteccem/material_matematicas.pdf